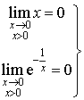Enoncé
3) La fonction
 est définie sur
est définie sur
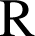 par
par 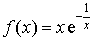 si
si
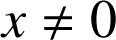 et
et
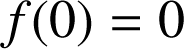 .
.
Résultat
Correction
Explications
A. 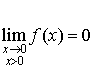
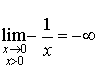 et
et ![]() d'où :
d'où :
B. 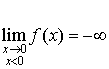

A l'aide du changement de variable ![]() ,
, 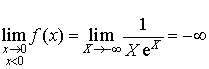 (d'après le cours
(d'après le cours ![]() et si
et si
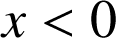 alors
alors ![]() ).
).
C. La fonction
 est continue en zéro
est continue en zéro
La fonction
 est définie en zéro (
est définie en zéro (
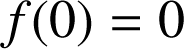 ) mais elle n'a pas pour limite zéro en zéro d'après les résultats des propositions A et B.
) mais elle n'a pas pour limite zéro en zéro d'après les résultats des propositions A et B.
D. La fonction
 est dérivable à droite en zéro et
est dérivable à droite en zéro et
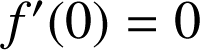
La fonction
 est définie en zéro et
est définie en zéro et 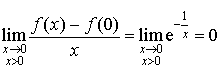 (résultat justifié en A) donc elle est dérivable à droite en zéro et
(résultat justifié en A) donc elle est dérivable à droite en zéro et ![]() .
.
E. La fonction
 est dérivable en zéro
est dérivable en zéro
Si
 était dérivable en zéro alors elle serait continue en zéro (propriété du cours) or, d'après la proposition C, elle n'est pas continue en zéro.
était dérivable en zéro alors elle serait continue en zéro (propriété du cours) or, d'après la proposition C, elle n'est pas continue en zéro.
L'étude directe donne 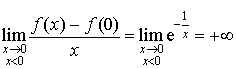 donc
donc
 n'est dérivable à gauche en zéro et n'est donc pas dérivable en zéro.
n'est dérivable à gauche en zéro et n'est donc pas dérivable en zéro.
F. Pour tout ![]() ,
, 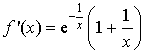 .
.
La fonction ![]() est dérivable sur
est dérivable sur
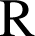 et la fonction
et la fonction 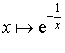 est dérivable sur
est dérivable sur
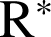 en tant que composée de la fonction
en tant que composée de la fonction ![]() dérivable sur
dérivable sur
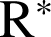 et de la fonction exponentielle dérivable sur
et de la fonction exponentielle dérivable sur
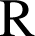 . La fonction
. La fonction
 est donc dérivable sur
est donc dérivable sur
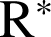 en tant que produit de deux fonctions dérivables sur
en tant que produit de deux fonctions dérivables sur
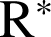 .
.
Pour tout ![]() ,
, 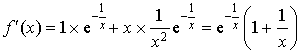 .
.