Enoncé
4) La fonction
est définie sur
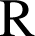par 
.
Résultat
Correction
Explications
A. Pour tout
,
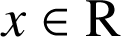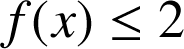
et 
B. Dans un repère orthonormal 
, la courbe d'équation
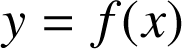admet une asymptote parallèle à l'axe des abscisses
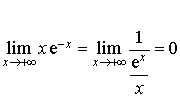(d'après le cours 
) donc 
; la droite d'équation
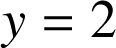est donc asymptote à la courbe d'équation
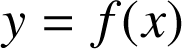au voisinage de
.
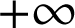C. La fonction
admet un maximum
L'étude des variations de
(pour tout 
, 
) justifie que
admet un maximum en 1. En effet,
est croissante sur
(
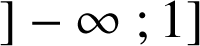) et décroissante sur
(
).
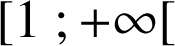D. Le tableau de variation de
est :
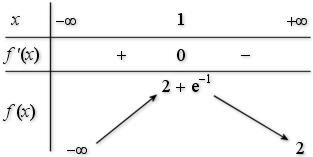
Tableau de variation de f
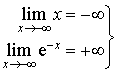
L'étude du tableau de variation de
permet de conclure que l'équation
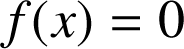admet une seule solution sur
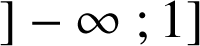et aucune sur
.
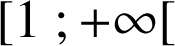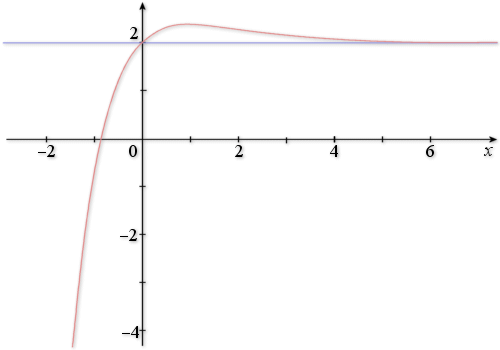
Représentation graphique de f