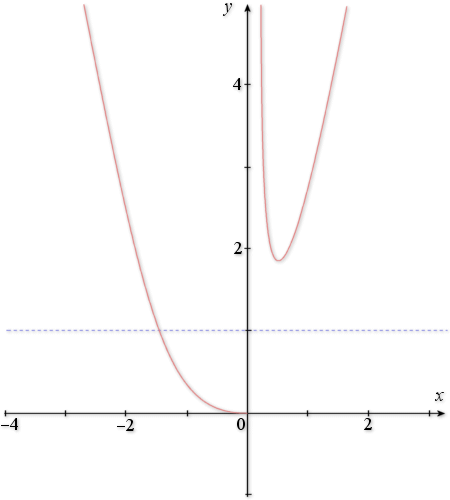
Enoncé
5) La fonction
est définie sur
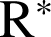par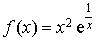 
.
Résultat
Correction
Explications
A. Pour tout
,
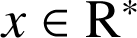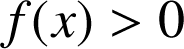
Pour tout
,
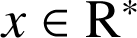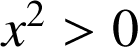et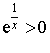 
.
B. Pour tout
, 
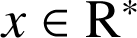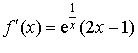
La fonction 
est dérivable sur
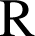donc sur
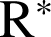et la fonction 
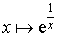est dérivable sur
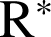en tant que composée de la fonction inverse dérivable sur
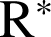et de la fonction exponentielle dérivable sur
.
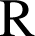est donc dérivable sur
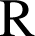en tant que produit de 2 fonctions dérivables sur
.
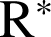Pour tout
, 
.
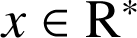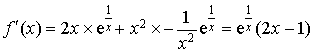C.
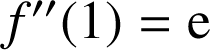
La fonction affine 
est dérivable sur
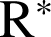et la fonction 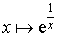est dérivable sur
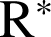(voir la proposition B) d'où la fonction
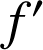est dérivable sur
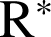(produit de 2 fonctions dérivables sur
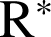) et pour tout
, 
.
.
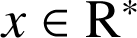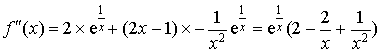D. L'équation
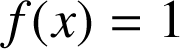admet 2 solutions dans
L'étude des variations de
justifie que
admet sur
un minimum égal à 
soit 
(
est décroissante sur 
et croissante sur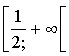 
) ; ce minimum est strictement supérieur à
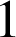donc l'équation
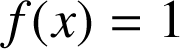n'a pas de solution dans
.
