Enoncé
2) Soit
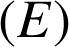l'équation : 
. Dans
:
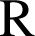Résultat
Correction
Explications
Dans
, 
(
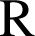et 
).
A l'aide du changement de variable 
, 
.
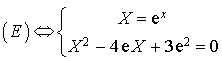Le polynôme du second degré 
a pour discriminant 
; il a donc 2 racines strictement positives 
et 
.
La fonction exponentielle est continue et strictement monotone de
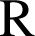dans
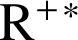d'où quel que soit le réel strictement positif
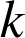, l'équation
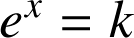admet une seule solution dans
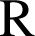d'après le théorème des valeurs intermédiaires.
On en déduit que
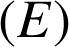admet exactement deux solutions dans
.
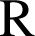