Définition
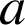et
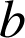désignent deux réels.
Résoudre l'équation différentielle
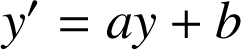sur
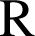, c'est trouver toutes les fonctions
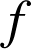dérivables sur
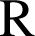telles que, pour tout
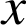de
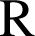, on a :
.
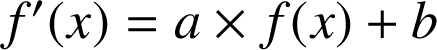Théorème
Si
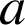et
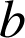sont des réels et
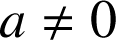, les solutions de
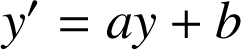sont les fonctions définies sur
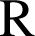par 
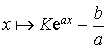où
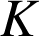désigne une constante réelle.Si
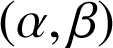est un couple de réels, l'équation
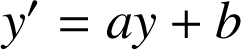admet une seule solution
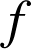vérifiant
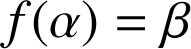.Les solutions de
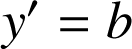sont les fonctions définies sur
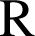par 
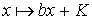où
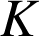désigne une constante réelle.
