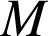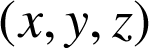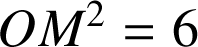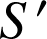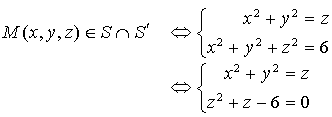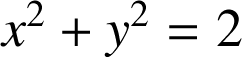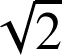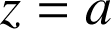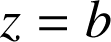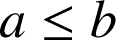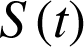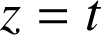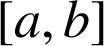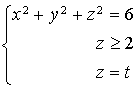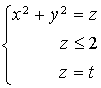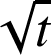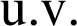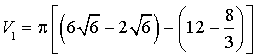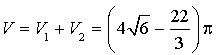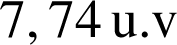Introduction
Durée : 45 minutes
Niveau : moyen
L'espace est muni d'un repère orthonormal 
;
est la sphère de centre
et de rayon
;
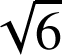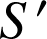est la surface d'équation
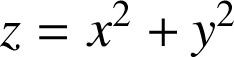dans 
.
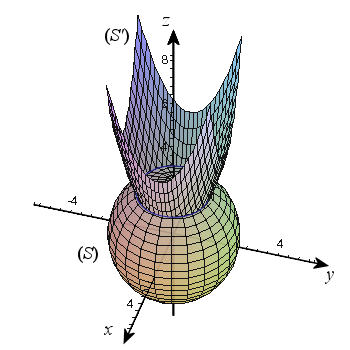
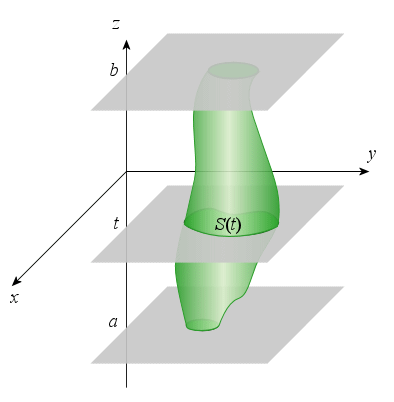
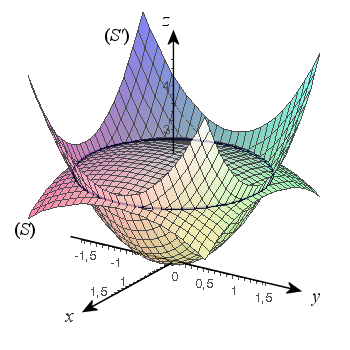
3) Le but de cette question est de calculer le volume
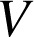de la partie de l'espace limitée par
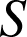et
.
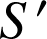On admet que
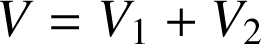avec,
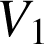volume de la partie de l'espace limitée par la calotte sphérique (
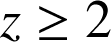) et le plan d'équation
,
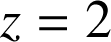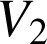volume de la partie de l'espace limitée par le tronc de paraboloïde (
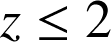) et le plan d'équation
.
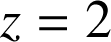Déterminer
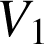et
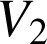puis en déduire une valeur approchée de
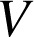en
.
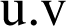