Introduction
Durée : 90 minutes
Niveau : moyen
Énoncé de l'exercice
Les parties (A), (B), et (C) sont indépendantes.
L'espace est muni d'un repère orthonormal ![]() .
.
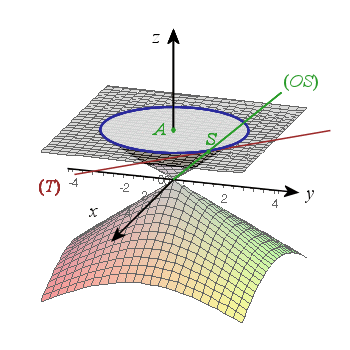
Les surfaces
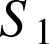 et
et
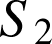 ont pour équation cartésienne dans
ont pour équation cartésienne dans ![]() respectivement :
respectivement : ![]() et
et ![]() .
.
1)
a. Soit
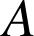 le point de coordonnées
le point de coordonnées
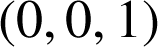 ; déterminer une équation de
; déterminer une équation de
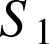 dans le repère
dans le repère ![]() . En déduire la nature de
. En déduire la nature de
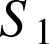 .
.
b. Montrer que
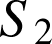 est un cône dont vous préciserez le sommet et l'axe.
est un cône dont vous préciserez le sommet et l'axe.
a. Les formules de changement de repère sont obtenues à l'aide de la relation vectorielle ![]() .
.
a. Si
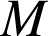 a pour coordonnées
a pour coordonnées
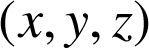 dans
dans ![]() et
et
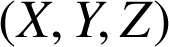 dans
dans ![]() alors
alors 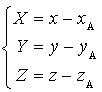 .
.
1) a. Le nouveau repère ![]() ayant pour origine le point
ayant pour origine le point
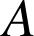 de coordonnées
de coordonnées
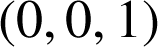 dans le repère
dans le repère ![]() , si
, si
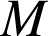 a pour coordonnées
a pour coordonnées
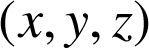 dans
dans ![]() et
et
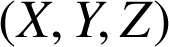 dans
dans ![]() alors
alors 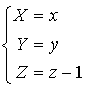 .
.
D'où ![]() .
.
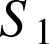 est un cône de sommet l'origine
est un cône de sommet l'origine
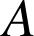 du repère
du repère ![]() et d'axe
et d'axe ![]() .
.
1) b. En utilisant la même démarche qu'à la question 1.a/, et en se plaçant dans le repère ![]() où ,
où ,![]() l'équation de
l'équation de
 dans ce repère est
dans ce repère est ![]() , équation d'un cône de sommet
, équation d'un cône de sommet
 et d'axe
et d'axe ![]() .
.
2) Peut-on trouver un plan
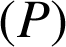 parallèle au plan
parallèle au plan ![]() qui coupe
qui coupe
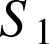 et
et
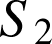 suivant le même cercle ?
suivant le même cercle ?
Quelle est l'équation cartésienne du cercle intersection d'un cône d'équation ![]() par le plan d'équation cartésienne
par le plan d'équation cartésienne
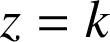 ?
?
2) Soit
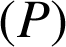 le plan cherché parallèle au plan
le plan cherché parallèle au plan ![]() donc d'équation
donc d'équation
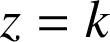 .
.
Soit ![]() . Le plan
. Le plan
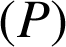 est muni du repère
est muni du repère ![]() .
.
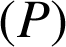 coupe les cônes
coupe les cônes
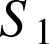 et
et
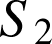 suivant les cercles d'équations respectives
suivant les cercles d'équations respectives ![]() et
et ![]() .
.
Ces deux cercles sont égaux si et seulement si ![]() , soit
, soit ![]() .
.
Cette dernière équation a deux solutions :
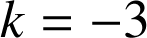 ou
ou
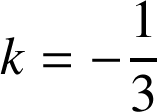 donc deux plans répondent au problème, les plans d'équation
donc deux plans répondent au problème, les plans d'équation
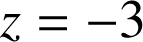 ,
,
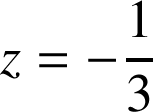 .
.
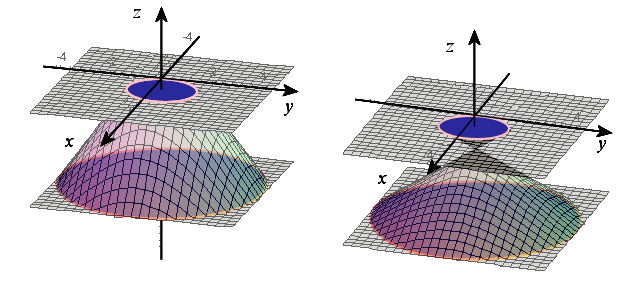
Un cône ![]() admet dans
admet dans ![]() pour équation cartésienne
pour équation cartésienne ![]() .
.
On appelle ![]() la courbe représentative de l'intersection de
la courbe représentative de l'intersection de ![]() par le plan
par le plan
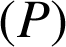 d'équation cartésienne
d'équation cartésienne
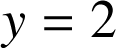 .
.
1) Déterminer le repère ![]() du plan
du plan
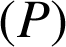 dans lequel
dans lequel ![]() est la réunion des deux courbes d'équation
est la réunion des deux courbes d'équation ![]() ,
, ![]() .
.
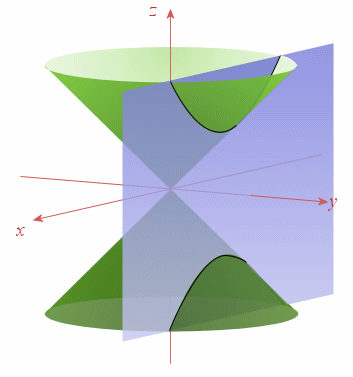
L'intersection ![]() d'un cône de sommet
d'un cône de sommet
 et d'axe
et d'axe ![]() par un plan d'équation
par un plan d'équation
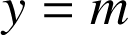 est caractérisé par :
est caractérisé par :
Dans ![]() ,
, 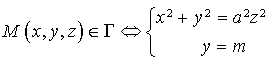 .
.
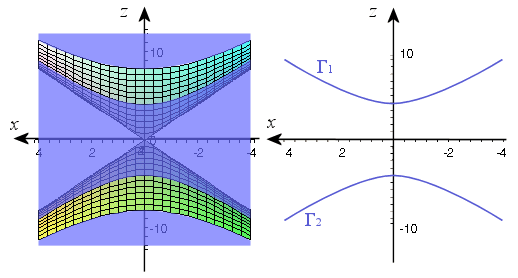
Intersection d'un cône
Avec un plan d'équation
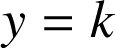 (
(
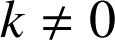 ) : c'est une hyperbole
) : c'est une hyperbole
1) Soit
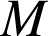 de coordonnées
de coordonnées
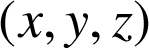 dans
dans ![]() ,
, 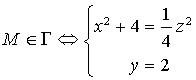 .
.
D'où si
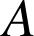 a pour coordonnées dans
a pour coordonnées dans ![]()
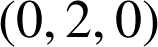 alors dans le plan
alors dans le plan
 muni du repère
muni du repère ![]() ,
, ![]() a pour équation cartésienne
a pour équation cartésienne ![]() .
.
![]() est donc la réunion des deux courbes d'équation
est donc la réunion des deux courbes d'équation ![]() ,
, ![]() .
.
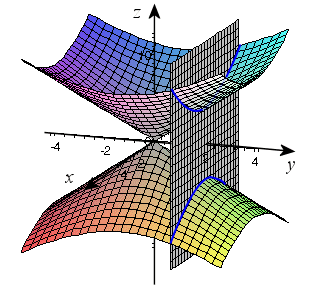
2) Soit
 la fonction définie par
la fonction définie par ![]() pour
pour ![]() et
et ![]() sa représentation graphique dans le repère
sa représentation graphique dans le repère ![]() :
:
a. Étudier la parité de
 .
.
b. Déterminer ![]() et montrer que la droite d'équation
et montrer que la droite d'équation
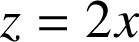 est une asymptote de
est une asymptote de ![]() au voisinage de
au voisinage de
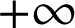 .
.
c. Établir le tableau de variation de
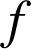 sur
sur
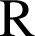 . Préciser une équation de l'asymptote de
. Préciser une équation de l'asymptote de ![]() au voisinage de
au voisinage de
 . Construire
. Construire ![]() .
.
d. Soit
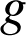 la fonction définie par
la fonction définie par ![]() pour
pour ![]() et
et ![]() sa représentation graphique dans le repère
sa représentation graphique dans le repère ![]() .
.
Justifier que ![]() est symétrique de
est symétrique de ![]() par rapport à l'axe
par rapport à l'axe ![]() .
.
Construire ![]() .
.
b. La droite d'équation
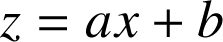 est asymptote à la courbe représentative de
est asymptote à la courbe représentative de
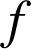 d'équation
d'équation
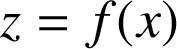 au voisinage de
au voisinage de
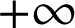 si
si ![]() .
.
b. Montrer que 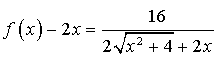 .
.
2) a. Pour tout ![]() ,
, ![]() ; la fonction
; la fonction
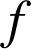 est donc paire.
est donc paire.
2) b. 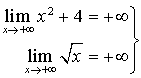 donc
donc ![]() et donc
et donc ![]() .
.
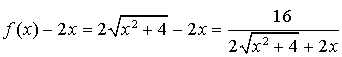 (le changement d'écriture en multipliant par le conjugué est nécessaire car avec l'écriture sous forme de différence il n'est pas possible de conclure sur la limite cherchée).
(le changement d'écriture en multipliant par le conjugué est nécessaire car avec l'écriture sous forme de différence il n'est pas possible de conclure sur la limite cherchée).
![]() donc
donc ![]() .
.
![]() donc la droite d'équation
donc la droite d'équation
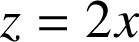 est asymptote à
est asymptote à ![]() au voisinage de
au voisinage de
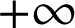 .
.
2) c. La fonction ![]() est croissante et strictement positive sur
est croissante et strictement positive sur ![]() et la fonction
et la fonction ![]() est croissante sur
est croissante sur ![]() donc la fonction
donc la fonction ![]() est croissante sur
est croissante sur ![]() et
et
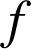 est croissante sur
est croissante sur ![]() .
.
La fonction
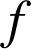 étant paire, le tableau de variation de
étant paire, le tableau de variation de
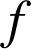 est donc :
est donc :
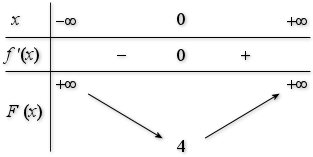
La fonction
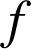 étant paire, la droite d'équation
étant paire, la droite d'équation
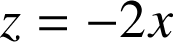 est asymptote à
est asymptote à ![]() au voisinage de
au voisinage de
 .
.
2) d. ![]() est la représentation graphique de
est la représentation graphique de
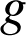 dans
dans ![]() et pour tout
et pour tout ![]() ,
, ![]() donc
donc ![]() et
et ![]() est la courbe symétrique de
est la courbe symétrique de ![]() par rapport à l'axe des ordonnées soit
par rapport à l'axe des ordonnées soit ![]() .
.
3) Soit ![]() et
et ![]() deux vecteurs, justifier que si un point
deux vecteurs, justifier que si un point
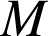 de
de
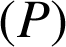 a pour coordonnées
a pour coordonnées
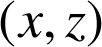 dans le repère
dans le repère ![]() et
et
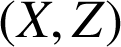 dans le repère
dans le repère ![]() alors
alors 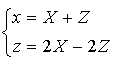 .
.
En déduire une équation de ![]() dans le repère
dans le repère ![]() .
.
Dire que
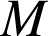 a pour coordonnées
a pour coordonnées
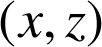 dans le repère
dans le repère ![]() et
et
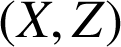 dans le repère
dans le repère ![]() signifie que
signifie que ![]() ; les coordonnées d'un point dans un repère donné sont uniques.
; les coordonnées d'un point dans un repère donné sont uniques.
3) Si
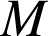 est un point de
est un point de
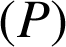 ,
, ![]() d'où,
d'où,
Les coordonnées de
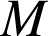 dans le repère
dans le repère ![]() étant uniques,
étant uniques, 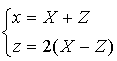 .
.
D'où l'équation de ![]() dans le repère
dans le repère ![]() étant
étant ![]() , dans le repère
, dans le repère ![]() , elle devient
, elle devient ![]() .
.
Après simplification, ![]() a pour équation dans
a pour équation dans ![]() ,
, ![]() (équation d'une hyperbole).
(équation d'une hyperbole).
Un cône ![]() admet dans
admet dans ![]() pour équation cartésienne
pour équation cartésienne ![]() .
.
1)
a. On appelle ![]() le cercle, intersection du cône
le cercle, intersection du cône ![]() par le plan
par le plan
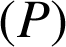 d'équation
d'équation
 ; déterminer une équation cartésienne de
; déterminer une équation cartésienne de ![]() dans le plan
dans le plan
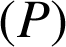 muni du repère
muni du repère ![]() où
où ![]() .
.
b. Déterminer une équation cartésienne, dans le plan
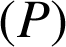 muni du repère
muni du repère ![]() , de la tangente
, de la tangente
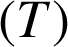 à
à ![]() en
en
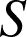 ,
,
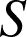 point d'abscisse
point d'abscisse
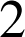 et d'ordonnée positive.
et d'ordonnée positive.
c. Justifier que les droites
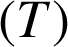 et
et
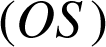 sont coplanaires et déterminer une équation cartésienne dans
sont coplanaires et déterminer une équation cartésienne dans ![]() du plan
du plan
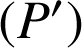 qu'elles déterminent.
qu'elles déterminent.
b. On se place dans le plan
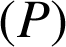 et
et
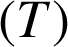 est la tangente en
est la tangente en
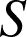 au cercle d'équation
au cercle d'équation
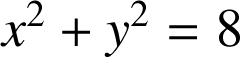 dans le repère
dans le repère ![]() ; on peut calculer les coordonnées de
; on peut calculer les coordonnées de
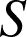 .
.
c. Deux droite sécantes de l'espace déterminent un plan ; si ![]() et
et ![]() sont des vecteurs directeurs respectivement de chacune de ces deux droites alors tout vecteur à la fois orthogonal à
sont des vecteurs directeurs respectivement de chacune de ces deux droites alors tout vecteur à la fois orthogonal à ![]() et à
et à ![]() est un vecteur normal à ce plan.
est un vecteur normal à ce plan.
b. Quel rôle joue ![]() pour
pour
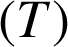 ?
?
1) a. Dans ![]() ,
, 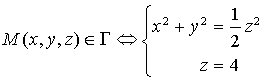
D'où si
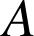 a pour coordonnées
a pour coordonnées
 , dans le plan
, dans le plan
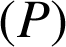 muni du repère
muni du repère ![]() ,
, ![]() a pour équation
a pour équation ![]() .
.
1) b. Dans
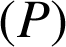 muni du repère
muni du repère ![]() ,
,
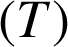 est perpendiculaire à la droite
est perpendiculaire à la droite
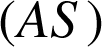 en
en
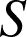 , elle est donc définie par le point
, elle est donc définie par le point
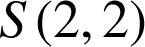 et le vecteur normal
et le vecteur normal ![]() , elle admet donc une équation cartésienne de la forme
, elle admet donc une équation cartésienne de la forme ![]() avec
avec ![]() soit
soit ![]() .
.
1) c. Les droites
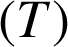 et
et
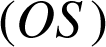 ont le point
ont le point
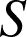 pour point commun et sont distinctes (
pour point commun et sont distinctes (![]() ), elles déterminent donc un plan unique
), elles déterminent donc un plan unique
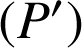 .
.
Dans ![]() , le vecteur
, le vecteur ![]() a pour coordonnées
a pour coordonnées
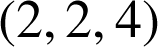 ; c'est un vecteur directeur de la droite
; c'est un vecteur directeur de la droite
 .
.
Dans ![]() , le vecteur
, le vecteur ![]() est un vecteur directeur de
est un vecteur directeur de
 .
.
Soit ![]() un vecteur orthogonal à
un vecteur orthogonal à ![]() et à
et à ![]() :
:
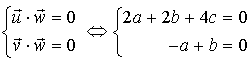
Soit pour
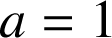 ,
, ![]() a pour coordonnées
a pour coordonnées
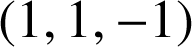 .
.
Le plan
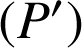 admet pour vecteur normal
admet pour vecteur normal ![]() ; il a donc une équation cartésienne de la forme
; il a donc une équation cartésienne de la forme ![]() .
.
![]() donc
donc
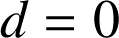 .
.
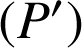 a pour équation cartésienne dans
a pour équation cartésienne dans ![]() ,
,
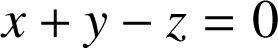 .
.
2) Démontrer que l'intersection du cône ![]() par le plan
par le plan
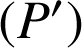 est défini dans
est défini dans ![]() par :
par :
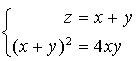
, soit par
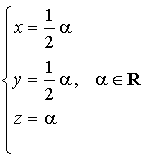
représentation paramétrique de la droite
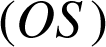 . Le plan
. Le plan
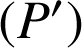 coupe donc le cône
coupe donc le cône ![]() suivant la droite
suivant la droite
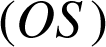 , il est tangent à
, il est tangent à ![]() le long de la génératrice
le long de la génératrice
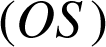 de
de ![]() .
.
Quelles sont les conditions vérifiées par les coordonnées
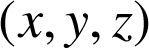 d'un point
d'un point
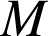 , pour que ce point appartienne à
, pour que ce point appartienne à ![]() et à
et à
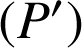 ?
?
2) Dans ![]() ,
, 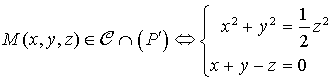
Soit, 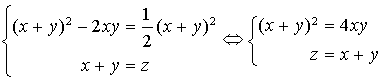
L'intersection du cône ![]() et du plan
et du plan
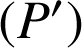 est défini dans
est défini dans ![]() par
par 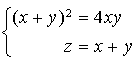 .
.
Soit ![]() ,
, ![]() ,
,



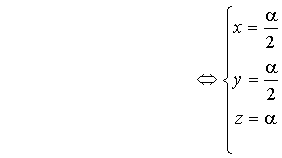
Ce système d'équations paramétrique est celui d'une droite passant par
 et de vecteur directeur le vecteur de composantes
et de vecteur directeur le vecteur de composantes 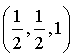 , soit le vecteur
, soit le vecteur ![]() .
.
C'est donc une représentation paramétrique de la droite
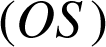 . Le plan
. Le plan
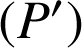 coupe donc
coupe donc ![]() suivant la droite
suivant la droite
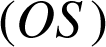 .
.