Enoncé
2) Le plan complexe est rapporté à un repère orthonormé direct ![]() .
.
Soit
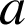 un complexe non nul, et distinct de
un complexe non nul, et distinct de
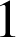 .
.
On appelle
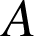 ,
,
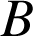 ,
,
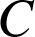 ,
,
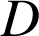 et
et
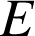 les points d'affixes
les points d'affixes
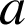 ,
,
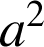 ,
,
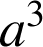 ,
,
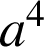 ,
,
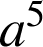 , et
, et
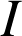 le point d'affixe
le point d'affixe ![]() .
.
Résultat
Correction
Explications
A.
Calculons ![]() ,
, ![]() ,
, ![]() .
.
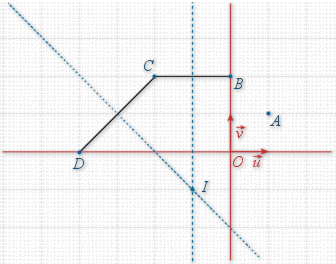
Il est facile de vérifier que le centre du cercle circonscrit au triangle
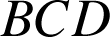 est le point
est le point
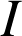 d'affixe
d'affixe ![]() car les distances
car les distances
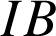 ,
,
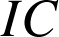 et
et
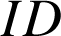 sont égales à
sont égales à
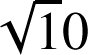 , et que la point
, et que la point
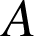 n'appartient pas à ce cercle car la distance
n'appartient pas à ce cercle car la distance
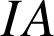 est égale à
est égale à
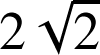 .
.
B.
C'est à l'évidence la similitude directe d'écriture complexe ![]() , donc une similitude directe de centre
, donc une similitude directe de centre
 , d'angle
, d'angle ![]() , et de rapport
, et de rapport ![]() .
.
C.
Soit ![]() le cercle auquel appartiennent
le cercle auquel appartiennent
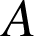 ,
,
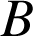 ,
,
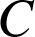 et
et
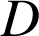 . Ce cercle est le cercle circonscrit au triangle
. Ce cercle est le cercle circonscrit au triangle
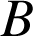 ,
,
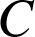 et
et
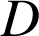 .
.
![]() contient
contient
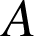 ,
,
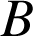 et
et
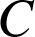 .
.
L'image de ![]() par la similitude
par la similitude
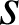 d'écriture complexe
d'écriture complexe ![]() passe par les images de
passe par les images de
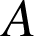 ,
,
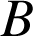 et
et
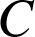 , donc par
, donc par
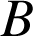 ,
,
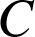 et
et
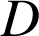 .
.
Donc ![]() .
.
Comme
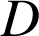 appartient au cercle
appartient au cercle ![]() , son image
, son image
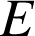 par
par
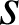 appartient au cercle
appartient au cercle ![]() .
.
D.
Comme
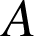 ,
,
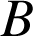 ,
,
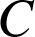 et
et
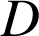 appartiennent à un même cercle, ce cercle
appartiennent à un même cercle, ce cercle ![]() est sa propre image par la similitude
est sa propre image par la similitude
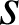 d'écriture complexe
d'écriture complexe ![]() . Si ce cercle a pour centre
. Si ce cercle a pour centre
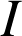 , alors
, alors ![]() , ce qui est faux (
, ce qui est faux (
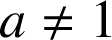 , donc le seul point invariant par
, donc le seul point invariant par
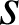 est
est
 ).
).
Remarque : l'image d'un cercle de rayon
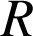 par une similitude de rapport
par une similitude de rapport
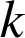 est le cercle de rayon
est le cercle de rayon
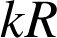 . Donc ici le rapport de la similitude est
. Donc ici le rapport de la similitude est
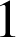 .
.
Il s'ensuit que ![]() . On a donc également
. On a donc également ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,ce qui montre que
,ce qui montre que ![]() .
.
Les points
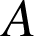 ,
,
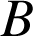 ,
,
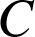 ,
,
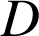 et
et
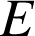 appartiennent au cercle de centre
appartiennent au cercle de centre
 et de rayon
et de rayon
 .
.