Enoncé
Soit
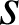la similitude d'écriture complexe 
(
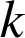est un réel strictement positif).
L'outil graphique suivant (cliquez ici) vous permet de visualiser l'image de
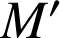par la transformation d'écriture complexe .
Vous pouvez déplacer le point
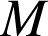et choisir la valeur de
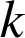dans l'intervalle
.
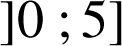Résultat
Correction
Explications
A.
Une rotation est une similitude directe. Or l'écriture complexe de
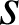est celle d'une similitude indirecte.
B.
Pour les mêmes raisons que précédemment, si
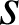est une réflexion, c'est une isométrie.
admet le point
comme point invariant. Soit 
un point du plan complexe, distinct de
, et 
son image par
. Pour que
soit une isométrie, il est nécessaire que 
, donc que :
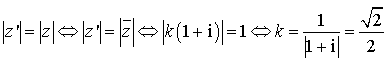
Réciproquement, si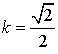 
, l'écriture complexe est 
.
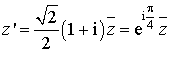Pour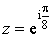 
, on a 
.
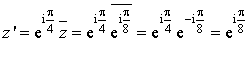Le point
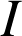d'affixe 
est invariant.
Comme pour
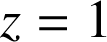, on a 
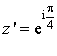, la similitude n'est pas l'identité. Puisqu'elle a deux points invariants (
et
),
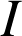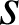est donc la réflexion d'axe
.
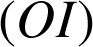C.
Prenons par exemple
.
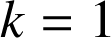L'écriture complexe de
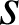est 
.
Posons 
.
Le point est invariant si et seulement si :
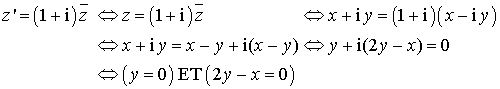
Il y a un seul point invariant qui est
.
Remarque : Étude du cas général
Posons .
Le point est invariant si et seulement si :
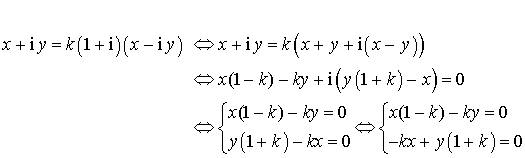
Ce système admet une unique solution si et seulement si :
(
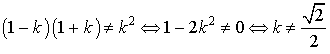
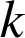est un réel strictement positif).
Il y a donc un seul point invariant pour toute valeur de
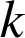distincte de 
.
Le système précédent est équivalent à :
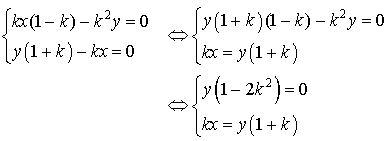
Pour
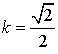, une solution est le point de coordonnées 
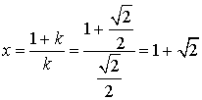et
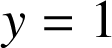. Il y a donc au moins deux points invariants (on sait que dans ce cas
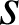est une réflexion).Pour
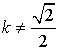, on a
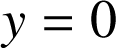et donc
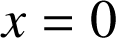. Il y a dans ce cas un seul point invariant qui est
.
D.
L'écriture complexe de
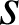est 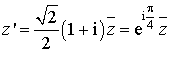, et celle de 
est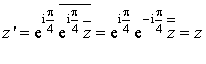 
.
est l'identité, c'est la rotation de centre
et d'angle nul.