Enoncé
3) Le plan complexe est rapporté à un repère orthonormé direct ![]() .
.
On considère les points ![]() ,
, ![]() , et
, et ![]() et
et ![]() .
.
On désigne respectivement par
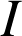 ,
,
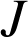 et
et
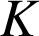 les milieux de
les milieux de ![]() ,
, ![]() et
et ![]() .
.
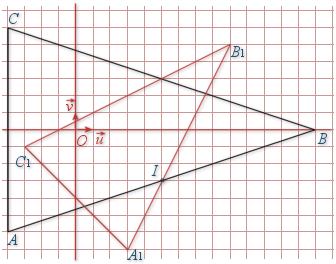
Soit
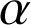 l'angle de la similitude directe de centre
l'angle de la similitude directe de centre
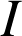 qui transforme
qui transforme
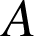 en
en
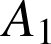 .
.
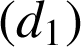 est l' image de la droite
est l' image de la droite
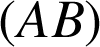 par la rotation de centre
par la rotation de centre
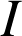 et d'angle
et d'angle
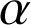 .
.
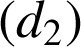 est l' image de la droite
est l' image de la droite
 par la rotation de centre
par la rotation de centre
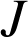 et d'angle
et d'angle
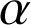 .
.
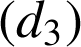 est l' image de la droite
est l' image de la droite
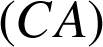 par la rotation de centre
par la rotation de centre
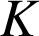 et d'angle
et d'angle
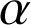 .
.
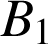 est le point d'intersection de
est le point d'intersection de
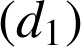 et
et
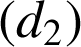 , et
, et
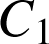 celui de
celui de
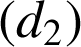 et
et
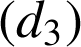 .
.
Résultat
Correction
Explications
A.
L'angle ![]() est un argument de
est un argument de 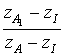 .
.
Le point
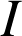 a pour affixe
a pour affixe ![]() .
.
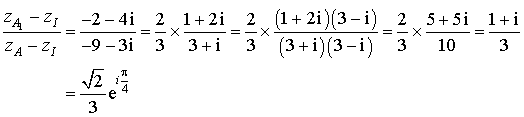
Par conséquent l'angle ![]() vaut
vaut ![]() .
.
Remarque : le rapport de similitude est ![]() .
.
B.
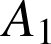 appartient à
appartient à
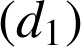 car l'angle
car l'angle 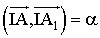 .
.Montrons que
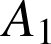 appartient à
appartient à
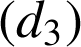 :
:
La droite
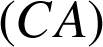 a pour équation
a pour équation
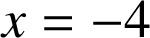 . Le point
. Le point
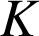 a pour coordonnées
a pour coordonnées
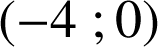 .
.
L'écriture complexe de la rotation de centre
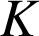 et d'angle
et d'angle ![]() est :
est : 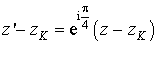 .
.
Soit
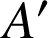 l'image de
l'image de
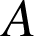 par cette rotation :
par cette rotation : 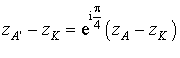 .
.
Calculons :
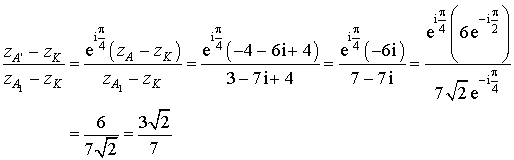
Donc 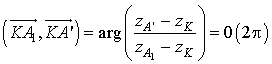 , ce qui montre que
, ce qui montre que
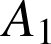 appartient à l'image de la droite
appartient à l'image de la droite
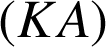 par la rotation de centre
par la rotation de centre
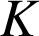 et d'angle
et d'angle ![]() , c'est-à-dire
, c'est-à-dire
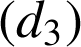 .
.
C.
Comme
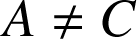 et
et
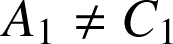 , il existe une similitude directe
, il existe une similitude directe
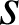 transformant
transformant
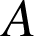 en
en
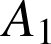 et
et
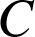 en
en
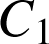 ; cette similitude a pour écriture complexe
; cette similitude a pour écriture complexe ![]() , avec
, avec ![]() et
et ![]() , donc :
, donc :
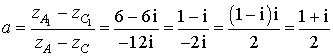
De plus :
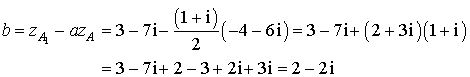
L'écriture complexe de la similitude directe transformant
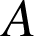 en et
en et
 en est
en est
On peut cependant vérifier que
 est l'image de
est l'image de
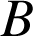 car :
car :
D.
Le centre de la similitude directe
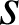 est le point
est le point ![]() , dont l'affixe est solution de :
, dont l'affixe est solution de :
Ce point n'est pas le milieu de
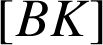 car
car ![]() .
.