Enoncé
2) Soit
 le point d'affixe
le point d'affixe ![]() et
et
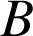 le point d'affixe
le point d'affixe
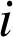 .
.
Soit
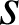 la réflexion d'axe
la réflexion d'axe ![]() .
.
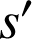 est la réflexion d'axe
est la réflexion d'axe ![]() .
.
Résultat
Correction
Explications
A.
Par la transformation d'écriture complexe ![]() :
:
 est invariant car
est invariant car 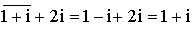 ,
,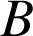 est invariant car
est invariant car 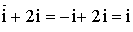 .
.
Donc cette transformation est une similitude, différente de l'identité, et ayant comme points fixes
 et
et
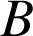 . D'après le cours, c'est bien la réflexion d'axe
. D'après le cours, c'est bien la réflexion d'axe ![]() .
.
B.
Par la transformation d'écriture complexe ![]() , le point
, le point
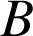 n'est pas invariant car
n'est pas invariant car ![]() .
.
REMARQUE :
si ![]() est l'écriture complexe de
est l'écriture complexe de
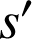 , on doit avoir :
, on doit avoir :
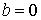 car
car
 est invariant par
est invariant par
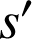 ,
,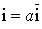 car
car
 est invariant par
est invariant par
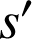 , donc
, donc 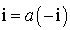
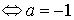 .
.
Donc l'écriture complexe de
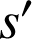 est
est ![]() .
.
C.
On a ![]() et
et ![]() , donc
, donc ![]() .
.
Donc
 n'et pas invariant par
n'et pas invariant par ![]() , qui ne peut pas être une similitude de centre
, qui ne peut pas être une similitude de centre
 .
.
D.
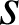 et
et
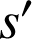 sont des similitudes indirectes, donc leur composée est une similitude directe.
sont des similitudes indirectes, donc leur composée est une similitude directe.
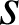 et
et
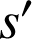 sont des isométries, donc leur composée est une isométrie.
sont des isométries, donc leur composée est une isométrie.
Le point d'intersection des axes de
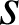 et
et
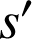 est invariant par
est invariant par ![]() .
.
![]() est une similitude directe, différente de l'identité ; d'après le cours, deux cas peuvent se présenter :
est une similitude directe, différente de l'identité ; d'après le cours, deux cas peuvent se présenter :
c'est une translation,
elle admet un point invariant
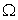 et elle est la composée commutative d'une homothétie de centre
et elle est la composée commutative d'une homothétie de centre 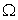 et de rapport
et de rapport
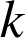 et d'une rotation (où
et d'une rotation (où
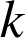 est le rapport de la similitude).
est le rapport de la similitude).
Le premier cas n'est pas possible puisque l'isométrie, différente de l'identité, a un point invariant.
Comme
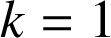 ,
, ![]() est une rotation.
est une rotation.