Enoncé
6) Soit
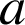 ,
,
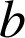 et
et
 trois entiers premiers strictement supérieurs à
trois entiers premiers strictement supérieurs à
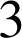 . Alors l'entier
. Alors l'entier ![]() n'est pas premier.
n'est pas premier.
Cliquez ici pour obtenir une aide.
Résultat
Correction
Explications
En étudiant des cas particuliers, on constate que
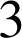 est toujours un diviseur de
est toujours un diviseur de ![]() .
.
Les seuls restes possibles dans la division euclidienne par
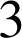 sont
sont
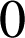 ,
,
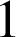 et
et
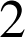 .
.
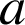 est premier strictement supérieur à
est premier strictement supérieur à
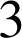 , donc
, donc ![]() ou
ou ![]() . Par suite, on a :
. Par suite, on a : ![]() . De même,
. De même, ![]() et
et ![]() . Par somme :
. Par somme : ![]() .
.
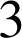 divise toujours
divise toujours ![]() , entier strictement supérieur à
, entier strictement supérieur à
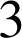 , donc
, donc ![]() n'est jamais premier.
n'est jamais premier.