Enoncé
4) Soit
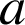et
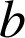deux entiers naturels premiers entre eux. On considère la suite 
définie par 
, 
et, pour tout
, 
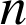. Alors deux termes consécutifs de sont premiers entre eux.
Cliquez ici pour obtenir une aide.
Résultat
Correction
Explications
Soit 
la proposition : « 
et 
sont premiers entre eux ».
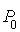est vraie.Si pour
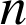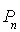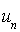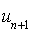entier naturel, est vraie alors et sont premiers entre eux et par suite, 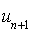et 
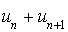sont premiers entre eux. Ainsi, 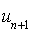et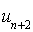 
sont premiers entre eux donc 
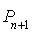est vraie.Conclusion : pour tout entier naturel
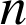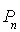, est vraie.