Enoncé
3) Soit
 ,
,
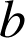 ,
,
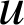 et
et
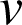 quatre entiers non nuls tels que
quatre entiers non nuls tels que
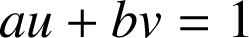 . On pose
. On pose
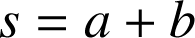 et
et
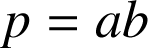 .
.
Résultat
Correction
Explications
A.
 et
et
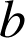 sont premiers entre eux
sont premiers entre eux
Il s'agit d'une application directe du théorème de Bézout.
B.
 et
et
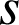 sont premiers entre eux
sont premiers entre eux
Soit
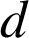 un diviseur commun à
un diviseur commun à
 et
et
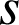 alors
alors
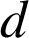 divise
divise
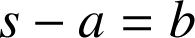 . Ainsi
. Ainsi
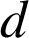 divise
divise
 et
et
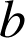 premiers entre eux, donc
premiers entre eux, donc
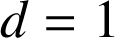 .
.
C.
 et
et
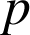 sont premiers entre eux
sont premiers entre eux
C'est faux si
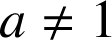 .
. ![]() .
.
D.
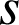 et
et
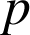 sont premiers entre eux
sont premiers entre eux
Si
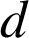 divise
divise
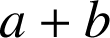 et
et
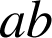 , il divise aussi
, il divise aussi ![]() , donc
, donc
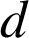 divise
divise
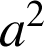 . De même,
. De même,
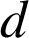 divise
divise
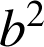 ; or du fait que
; or du fait que
 et
et
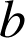 sont premiers entre eux,
sont premiers entre eux,
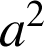 et
et
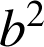 sont premiers entre eux, donc
sont premiers entre eux, donc
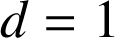 . Ainsi,
. Ainsi, ![]() .
.