Enoncé
4) Soit
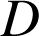 le
le
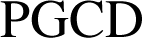 des entiers naturels
des entiers naturels
 et
et
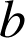 avec
avec
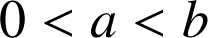 .
.
Résultat
Correction
Explications
A. ![]()
Soit ![]() . Si
. Si
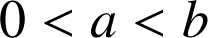 alors
alors
 ,
,
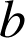 et
et
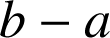 sont des entiers naturels non nuls.
sont des entiers naturels non nuls.
Si
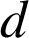 divise
divise
 et
et
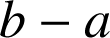 , alors
, alors
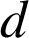 divise
divise
 et
et ![]() .
.
Inversement, si
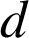 divise
divise
 et
et
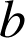 , alors
, alors
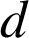 divise
divise
 et
et
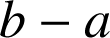 .
.
Ainsi, les diviseurs communs de
 et
et
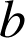 sont les diviseurs communs de
sont les diviseurs communs de
 et
et
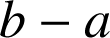 . D'où
. D'où ![]() .
.
B. ![]()
Contre-exemple : ![]() or
or ![]() .
.
C. ![]()
Si
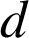 divise
divise
 et
et
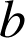 , alors
, alors
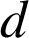 divise
divise ![]() et
et ![]() , combinaisons linéaires à coefficients entiers de
, combinaisons linéaires à coefficients entiers de
 et
et
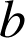 .
.
Inversement, si
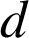 divise
divise ![]() et
et ![]() , alors
, alors
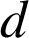 divise
divise ![]() et
et ![]() .
.
Ainsi, les diviseurs communs de
 et
et
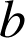 sont les diviseurs communs de
sont les diviseurs communs de ![]() et
et ![]() . D'où l'égalité des
. D'où l'égalité des
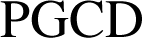 .
.
D. ![]() est divisible par
est divisible par ![]()
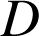 divise
divise
 et
et
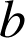 donc
donc ![]() divise
divise
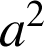 et
et
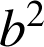 , puis
, puis ![]() divise
divise ![]() .
.