Enoncé
2) Pour tout entier naturel
:
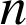Résultat
Correction
Explications
A. 
est pair
Si
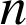est pair alors est pair.
Si
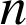est impair alors
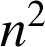est impair donc 
est pair, puis .
B. est multiple de
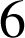
Contre-exemple : pour
, 
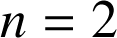et
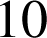n'est pas un multiple de
.
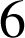C. 
est multiple de
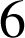
Le produit de deux entiers consécutifs est multiple de
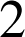, puisque l'un des entiers est pair.
Le produit de trois entiers consécutifs est multiple de
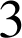, puisque l'un des entiers est multiple de
.
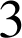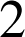et
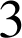sont premiers entre eux donc est multiple de
.
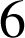D. 
est multiple de
Soit 
.
D'après la proposition précédente, est multiple de
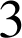donc
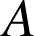est multiple de
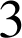. De plus, 
, produit de 4 entiers consécutifs, est multiple de
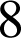. En effet, l'un des facteurs est multiple de
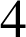et l'un des trois autres est nécessairement pair.
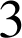et
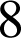étant premiers entre eux, est multiple de
.