Déterminer les couples
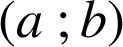 d'entiers naturels vérifiant
d'entiers naturels vérifiant
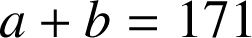 et
et ![]() .
.
On pose ![]() .
.
Il existe donc deux entiers naturels
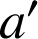 et
et
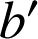 premiers entre eux tels que :
premiers entre eux tels que :
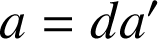 et
et
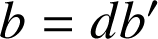 .
.
De plus ![]() .
.
Par conséquent
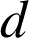 divise
divise
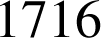 et
et
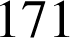 . Or
. Or ![]() ; donc
; donc
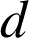 divise
divise
 .
.
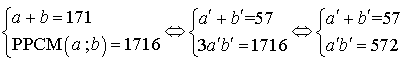
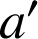 et
et
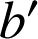 sont deux diviseurs propres de
sont deux diviseurs propres de
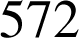 dont la somme est
dont la somme est
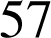 et le produit
et le produit
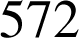 .
.
Si
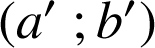 est solution de ce système alors
est solution de ce système alors
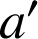 et
et
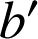 sont les solutions de l'équation du second degré :
sont les solutions de l'équation du second degré : ![]() .
.
Cette équation possède deux solutions entières :
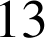 et
et
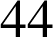 .
.
Il y a deux couples solutions
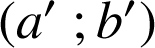 :
:
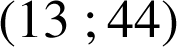 et
et
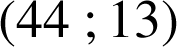 .
.
Il y a deux couples solutions
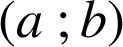 :
:
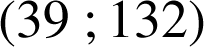 et
et
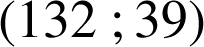 .
.
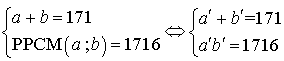
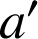 et
et
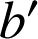 sont deux diviseurs propres de
sont deux diviseurs propres de
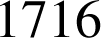 dont la somme est
dont la somme est
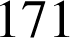 et le produit
et le produit
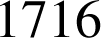 .
.
Si est solution de ce système alors
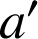 et
et
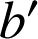 sont les solutions de l'équation du second degré :
sont les solutions de l'équation du second degré : ![]() .
.
Cette équation ne possède pas de solutions entières donc il n'y a pas de couples
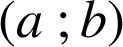 solutions.
solutions.
il y a deux couples solutions
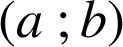 :
:
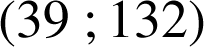 et
et
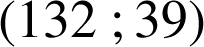 .
.






