Définition
Soit
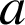un entier relatif quelconque, soit
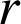le reste dans la division euclidienne de
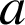par
:
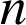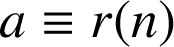où 
.
Exemple
Par conséquent dans la congruence modulo
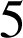, on rencontre 5 cas :
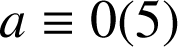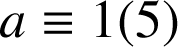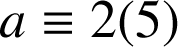ou
ou
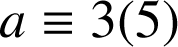ou
ou
.
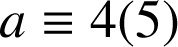