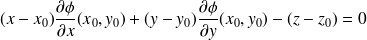La surface 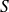est caractérisée par une équation cartésienne implicite :

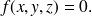
On suppose que 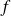est différentiable en 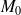. On note

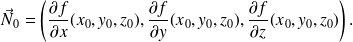
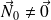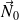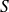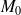On suppose que$ , alors est un vecteur normal à en , d'où l'équation du plan tangent à 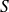en :

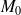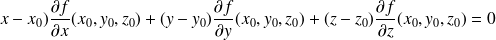
Un vecteur normal à une surface en un point est un vecteur normal au plan tangent à la surface en ce point.

Soit 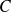une courbe tracée sur la surface 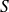et qui passe par 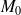. Si les équations paramétriques de 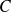sont :

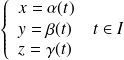
, on a donc

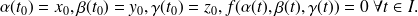
On suppose que les fonctions 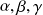sont dérivables, donc la courbe 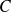admet un vecteur tangent en 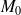qui est

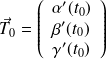
Appelons 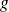la fonction d'une variable définie par 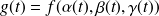. Puisque 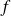est différentiable et que 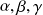sont dérivables, la fonction 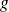est dérivable. Les résultats sur les dérivées des fonctions composées permettent de calculer la dérivée de :

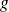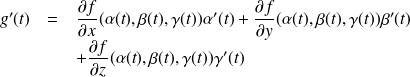
Donc en particulier .

Or

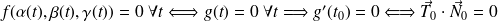
On en déduit que le vecteur 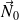est orthogonal à 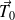, c'est \`a dire le vecteur 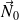est orthogonal au vecteur tangent \`a une courbe quelconque trac\'ee sur 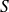et passant par 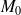. Ce vecteur 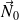est donc orthogonal au plan tangent à 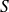en 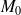, ce qui termine la démonstration.

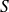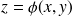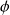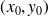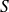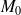La surface est caractérisée par une équation cartésienne explicite : , on suppose que est différentiable en alors l'équation du plan tangent à en est :