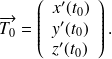Là encore, plusieurs types d'équation pour ces courbes :

1. Equations paramétriques d'une courbe de l'espace :

   Les équations paramétriques d'une courbe de l'espace sont données par :

   

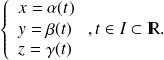
   Par abus de notation on note .

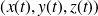   Par exemple la courbe dont les équations paramétriques sont :

   

2. Equations cartésiennes d'une courbe de l'espace.

   Une courbe de l'espace est l'intersection de 2 surfaces. Donc une courbe de l'espace est caractérisée par 2 équations de surfaces (implicites par exemple) :

   

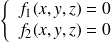
   Par exemple

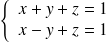
   est l'intersection de 2 plans, ce sont donc les équations cartésiennes d'une droite. Le passage entre les équations cartésiennes et les équations paramétriques d'une courbe n'est pas toujours évident.

Dans le cas d'une courbe paramétrée on pourrait faire une démonstration similaire à celle effectuée pour les courbes paramétrées du plan 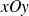et on obtiendrait un vecteur tangent à la courbe 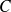au point :
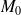