est une courbe munie d'une abscisse curviligne , appelons 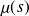la fonction qui définit la masse linéique en fonction de l'abscisse curviligne. On cherche à calculer la masse 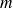de la partie de 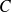comprise entre les points 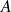et 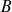d'abscisses curvilignes respectives 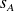et .

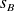On suppose 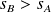(sinon on échange 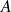et ).

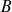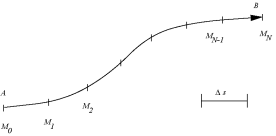
On discrétise le segment curviligne 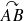, soit 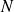un entier, on pose

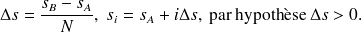
On note 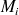le point d'abscisse curviligne 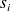, on a bien sûr 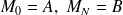. Voir figure \ref {fig3}

On note 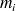la masse du segment curviligne 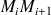, on peut écrire .

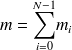Si 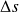est faible on peut supposer que la masse linéique varie peu sur le segment curviligne 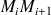, donc la masse du segment curviligne 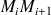est peu différente de 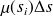. Pour être plus précis, on a :

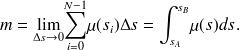
On retrouve en effet la définition de l'intégrale simple de Riemann.

On remarque que la masse 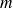est positive puisque la fonction 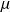est positive et que .

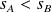Plus généralement si 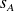et 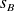sont quelconques, on a : .
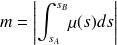