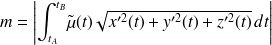Les objets comme les fils peuvent être modélisés par des courbes. Si la masse linéique
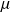 (masse par unité de longueur) est constante, alors la masse du fil de longueur
(masse par unité de longueur) est constante, alors la masse du fil de longueur
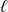 est égale à
est égale à
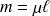 . La masse linéique n'est pas toujours constante (c'est le cas d'un fil dont la section ne serait pas constante). Supposons que l'on a défini une abscisse curviligne
. La masse linéique n'est pas toujours constante (c'est le cas d'un fil dont la section ne serait pas constante). Supposons que l'on a défini une abscisse curviligne
 sur la courbe
sur la courbe
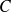 , appelons
, appelons
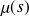 la fonction qui définit la masse linéique en fonction de l'abscisse curviligne. On cherche à calculer la masse
la fonction qui définit la masse linéique en fonction de l'abscisse curviligne. On cherche à calculer la masse
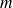 de la partie de
de la partie de
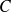 comprise entre les points
comprise entre les points
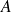 et
et
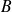 d'abscisses curvilignes respectives
d'abscisses curvilignes respectives
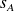 et
et
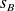 .
.
On montre alors que
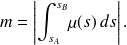
(Voir la démonstration dans le document référencé.)
Dans la pratique, on ne conna\^it pas toujours l'abscisse curviligne
 , mais plutôt une paramétrisation de
, mais plutôt une paramétrisation de
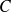
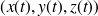 et la masse linéique est connue en fonction de
et la masse linéique est connue en fonction de
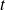 , on la note
, on la note
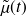 .
.
Si
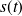 est la fonction qui définit l'abscisse curviligne en fonction de
est la fonction qui définit l'abscisse curviligne en fonction de
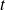 , on a la relation
, on a la relation
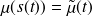 . En effectuant un changement de variables dans le calcul de
. En effectuant un changement de variables dans le calcul de
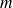 , on obtient donc la masse du fil d'extrémités
, on obtient donc la masse du fil d'extrémités
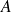 et
et
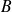 :
:
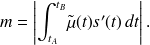
Soit
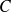 une courbe d'extrémités
une courbe d'extrémités
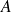 et
et
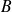 paramétrée par
paramétrée par
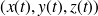 , on suppose que
, on suppose que
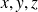 sont dérivables. On note
sont dérivables. On note
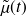 la masse linéique, alors la masse
la masse linéique, alors la masse
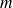 de
de
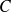 vaut :
vaut :