La notion d'intégrale curviligne, apparaît naturellement, comme une généralisation de l'intégrale d'une fonction d'une variable réelle. En effet, cette dernière peut être considérée comme une intégrale le long d'un segment 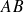. L'intégrale curviligne elle, sera une intégrale le long d'un arc de courbe joignant deux points du plan ou de l'espace. Dans ce chapitre, nous verrons trois applications qui conduisent à cette notion.

1. Calculer la longueur d'un segment de droite, du plan ou de l'espace, est un problème bien connu. Par extension, calculer la longueur d'une ligne brisée, c'est-à-dire d'un arc de courbe composée exclusivement de segments de droites est aussi un problème simple : il suffit d'additionner la longueur des segments composant la ligne brisée.

   Que faire maintenant pour une courbe plus générale ? On reprend le même type de technique que celui utilisé pour la définition de l'intégrale simple. Ici, on se donne un ensemble de points sur l'arc de courbe, pour joindre ces points par des segments de droite et on approche la longueur de cet arc de courbe par celle de la ligne brisée ainsi construite. Si lorsque l'on augmente le nombre de points, cette somme tend vers une limite indépendante du choix des points, il est alors raisonnable de considérer que cette limite représente la longueur de l'arc de courbe.

2. Deuxième problème ensuite, calculer la masse d'une courbe, connaissant sa masse par unité de longueur (linéique). Si cette masse linéique est constante, il suffit de la multiplier par la longueur de l'arc de courbe pour obtenir la masse désirée.

   Que faire maintenant dans le cas général ? On se donne à nouveau une subdivision de l'arc de courbe par des points, et l'on considère que la masse linéique est constante entre deux points consécutifs. En additionnant toutes les masses ainsi obtenues, on obtient une approximation de la masse de la courbe. Si lorsque l'on augmente le nombre de points de subdivision, cette somme tend vers une limite indépendante du choix des points, il est alors raisonnable de considérer que cette limite représente la masse de l'arc de courbe.

3. Troisième problème, en n, calculer le travail d'un champ de force appliquée à un point matériel se déplaçant le long d'un arc de courbe. Lorsque l'arc de courbe est un segment de droite et la force appliquée au point matériel est constante, il suffit de faire le produit scalaire de la force par le segment orienté dans le sens de parcours de la particule.

   Dans le cas général enfin, On se donne à nouveau une subdivision de l'arc de courbe par des points, et l'on approche la courbe par la ligne brisée reliant ces points. En outre, on suppose que la force est constante sur chaque segment de la ligne brisée. En additionnant tous les travaux ainsi obtenus, on obtient une approximation du travail du champ de force le long de l'arc de courbe parcouru par la particule. Si lorsque l'on augmente le nombre de points de subdivision, cette somme tend vers une limite indépendante du choix des points, il est alors raisonnable de considérer que cette limite représente le travail du champ de force.