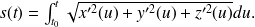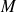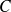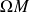On appelle abscisse curviligne du point de la courbe le nombre algébrique dont la valeur absolue est égale à la longueur de l'arc curviligne et dont le signe est celui du sens de parcours de

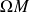
On utilise les notations et hypothèses. On va déterminer maintenant l'expression de 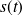. On sait déjà par définition que 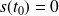puisque 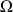est choisi comme origine.

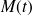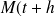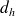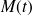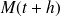Pour continuer on se ramène aux longueurs que l'on sait calculer, c'est à dire les longueurs de segments de droites. On fait l'hypothèse naturelle suivante, si et ) sont 2 points de la courbe, si on note la distance de à et 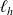la longueur du segment curviligne 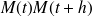alors ces deux infiniment petits sont équivalents , c'est à dire que 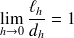. Voir figure \ref {fig2}

On suppose que la courbe est orientée dans le sens des 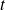croissants et que 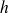est strictement positif. On a alors :

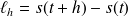
d'où :

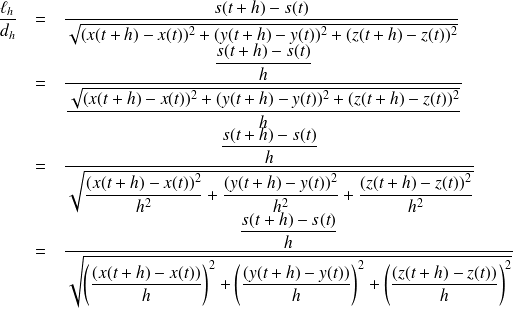
On obtient la même expression quand 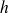est négatif.

On choisit donc maintenant 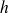de signe quelconque et on fait tendre 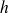vers zéro, on obtient donc en utilisant les résultats sur les limites :

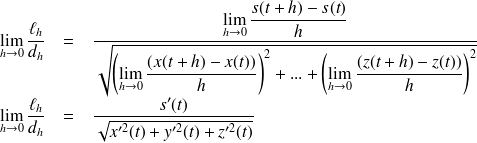
En appliquant l'hypothèse naturelle énoncée précédemment, cette limite vaut , donc on obtient :

.

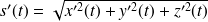On a donc :