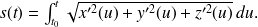Vous connaissez la notion d'abscisse sur une droite orientée, on peut généraliser cette notion à une courbe quelconque de la façon suivante. L'espace est muni d'un repère orthonormé
, soit
une courbe sans point double.
-
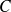est une courbe paramétrée par
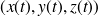, on note
. -
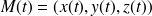Elle est orientée dans le sens des
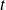croissants. -
On choisit une origine
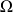sur
,
. -
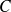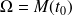On suppose que les fonctions
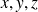sont dérivables.
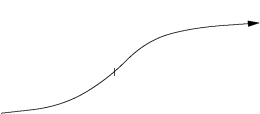
On peut alors définir l'abscisse curviligne de la façon suivante :
On appelle abscisse curviligne du point
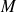de la courbe
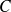le nombre algébrique
dont la valeur absolue est égale à la longueur de l'arc curviligne
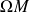et dont le signe est celui du sens de parcours de
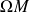(cf. figure ci-dessous).
On démontre, vous pouvez lire la démonstration en document, que
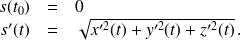
Donc
est la primitive de la fonction
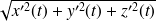qui s'annule en
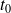. On peut donc écrire
sous la forme:
Avec les notations précédentes, l'abscisse curviligne
sur
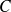est définie par :
