A partir de l'abscisse curviligne on peut définir la longueur d'un arc de courbe
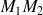, en effet :
Théorème
Soit
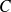une courbe paramétrée par
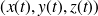, on suppose que
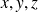sont dérivables, alors :
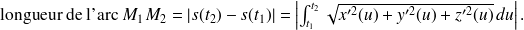
La longueur ne dépend ni de l'origine, ni de l'orientation choisie sur la courbe.
De plus, si la courbe est dans le plan
,
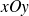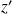est nulle et on peut appliquer la formule précédente.
Théorème
Soit
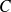une courbe du plan
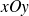dont l'équation polaire est
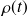, on suppose que
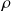est dérivable, alors
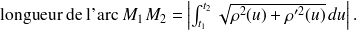
Démonstration
Une paramétrisation de la courbe est :
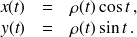
On a donc
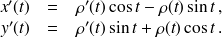
D'où
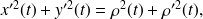
ce qui démontre le résultat.