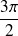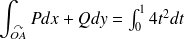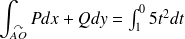On définit
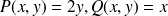 .
.
On définit
 ,
,
on note
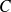 le bord de
le bord de
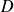 orienté dans le sens trigonométrique direct.
orienté dans le sens trigonométrique direct.
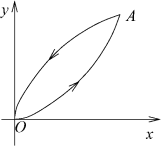
Faire une figure représentant
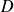 .
.
Calculer
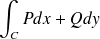 . (réponse :
. (réponse :
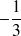 )
)
Il faut paramétrer
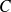 , donc il faut paramétrer
, donc il faut paramétrer
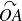 puis
puis
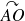 .
.
Pour
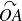 :
:
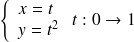 .
.
Pour
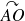 :
:
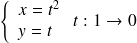 .
.
Utiliser la proposition \ref {circ} pour en déduire
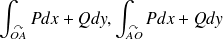 .
.
Après calculs on obtient :
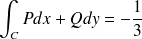
Calculer
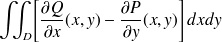
Exprimer l'intégrale double sur
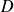 à l'aide d'intégrales simples, aidez-vous de la figure.
à l'aide d'intégrales simples, aidez-vous de la figure.
Calculez
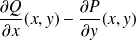
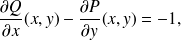
d'où
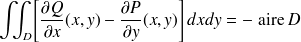
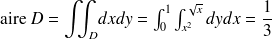
D'où le résultat.
On définit
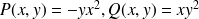 .
.
On définit
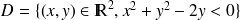 , on note
, on note
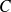 le bord de
le bord de
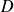 orienté dans le sens trigonométrique direct.
orienté dans le sens trigonométrique direct.
Faire une figure représentant
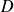 .
.
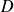 est le disque de centre
est le disque de centre
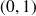 et de rayon
et de rayon
 .
.
Calculer
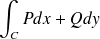 .
.
Il faut paramétrer
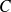 ,
,
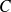 est un cercle.
est un cercle.
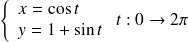 .
.
Utiliser la proposition
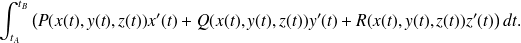 pour en déduire
pour en déduire
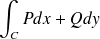 .
.
L'intégrale entre
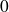 et
et
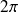 de
de
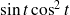 est nulle, faire le changement de variable
est nulle, faire le changement de variable
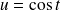 pour s'en convaincre. On linéarise les autres termes :
pour s'en convaincre. On linéarise les autres termes :
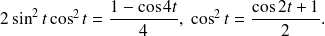
On n'oublie pas que l'intégrale d'un sinus ou d'un cosinus sur sa période est nulle, on obtient finalement :
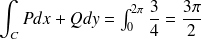
Calculer
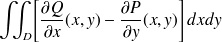
Exprimer l'intégrale double sur
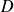 à l'aide d'un changement de variables.
à l'aide d'un changement de variables.
Calculez
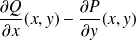
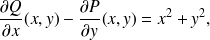
On peut utiliser les coordonnées polaires
 et
et
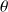 centrées en
centrées en
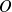 , cela simplifie la fonction à intégrer.
, cela simplifie la fonction à intégrer.
On peut également utiliser les coordonnées polaires
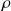 et
et
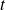 centrées en
centrées en
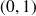 , cela simplifie le domaine d'intégration.
, cela simplifie le domaine d'intégration.
On obtient avec les coordonnées polaires centrées en
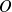 :
:
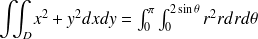
On obtient avec les coordonnées polaires centrées en
 :
:
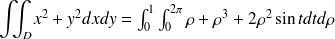
Bien sûr on obtient le même résultat dans les 2 cas :