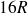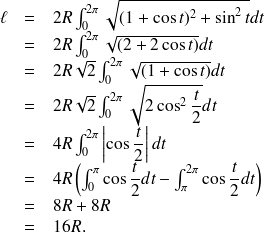La cardioïde est la courbe parcourue par un point
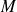 fixé sur un cercle mobile de rayon
fixé sur un cercle mobile de rayon
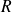 qui roule sans glisser à l'extérieur d'un cercle fixe de rayon
qui roule sans glisser à l'extérieur d'un cercle fixe de rayon
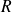 . On suppose que le cercle fixe est centré en
. On suppose que le cercle fixe est centré en
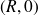 , que
, que
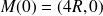 . On peut montrer que l'équation polaire de cette courbe est :
. On peut montrer que l'équation polaire de cette courbe est :
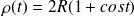
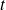 est l'angle dont a roulé le cercle. Lorsque
est l'angle dont a roulé le cercle. Lorsque
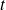 a varié de
a varié de
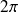 on a décrit toute la courbe, on est revenu au point de départ. La courbe a pour allure :
on a décrit toute la courbe, on est revenu au point de départ. La courbe a pour allure :
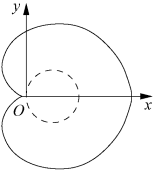
cardioide