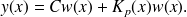Les cas les plus simples sont donnés par des équations différentielles linéaires à coefficients constants

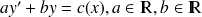
dont le second membre 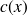est

• soit une fonction polynomiale ( 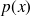), dans ce cas on cherche comme solution particulière une fonction polynomiale de même degré que ,

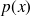• soit une exponentielle ( 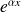), dans ce cas on cherche comme solution particulière une fonction de la forme ( 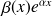). Si 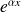n'est pas solution de l'équation homogène, alors 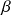est constante.

• soit une fonction trigonométrique ( et/ou 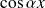), dans ce cas on cherche comme solution particulière une fonction trigonométrique ( ).

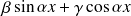Dans le cas général, en particulier lorsque les coefficients et 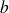ne sont pas des constantes, on utilise la méthode dite "variation de la constante" (paroxysme !). Elle consiste, à partir de la solution de l'équation homogène

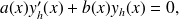
qui s'écrit sous la forme

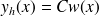
à considérer alors 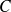comme une fonction de et à rechercher une solution particulière sous la forme

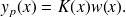
Écrire alors que 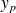est solution de l'équation avec second membre

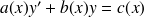
et montrer, en exercice, que 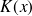est une primitive de 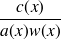. Comme le but est de calculer une solution particulière, on choisit une primitive particulière 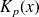et on obtiendra alors la solution générale de l'équation en faisant la somme de .
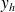
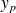