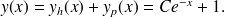On appelle équation différentielle linéaire du premier ordre, une équation de la forme
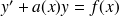
où
est une fonction définie sur
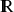ou une partie de
.
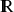On appelle équation homogène (ou équation sans deuxième membre) associée à
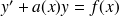l'équation
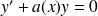
Cette équation est résolue de manière rigoureuse dans l'exercice de TD.
Sa solution est
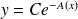
où
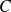est une constante quelconque et
une primitive de
.
La solution générale de
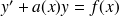peut s'écrire sous la forme
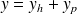
où
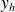est la solution générale de l'équation homogène
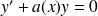et
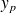est une solution particulière de l'équation "avec second membre''
.
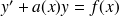(La démonstration de ce théorème est donnée en exercice.)
Par exemple, on veut résoudre l'équation
-
On résout l'équation homogène :
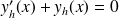
On remarque que
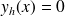est solution, on cherche maintenant les solutions non nulles, on peut donc diviser par
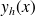.On obtient
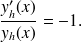En prenant une primitive, on a donc
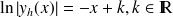, ou ce qui est équivalent en appliquant la fonction exponentielle : 
La constante
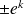est une constante strictement positive ou strictement négative.On peut résumer en écrivant
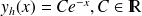. Pour
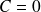on obtient la solution nulle, pour
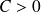, on a
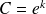, pour
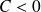, on a
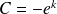.On a obtenu ainsi toutes les solutions de l'équation homogène. On dit que
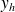est la solution générale de l'équation homogène. -
Une solution particulière de
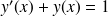est, par exemple,
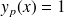(le vérifier !). -
Enfin, la solution générale de l'équation
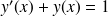est
