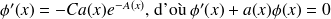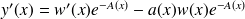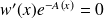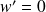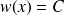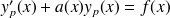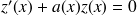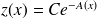-
Soit
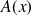une primitive quelconque de
et
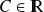, montrer alors que la fonction
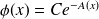
est solution de l'équation
.
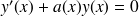2. Si on fait le changement de fonction inconnue en posant :
,
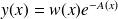quelle est l'équation vérifiée par
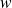? En déduire que toutes les solutions de
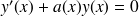sont de la forme
.
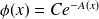3. Soient
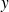la solution générale et
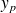une solution particulière de
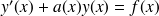
et soit
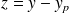. Déterminer l'équation dont
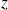est solution. En déduire que la solution générale de
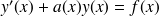est de la forme
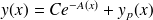
où
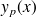est une solution particulière de
.
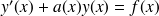