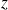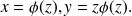Certaines équations peuvent se présenter sous la forme suivante :

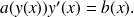
Dans ce cas on dit que l'équation est à variables séparées. Bien entendu, l'équation de départ ne se présente pas toujours sous la forme 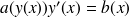mais, si on peut s'y ramener, on dit alors que l'équation est à variables séparables (nuance !).

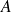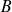Les solutions s'obtiennent en prenant des primitives par rapport à des deux membres de l'équation. Donc si est une primitive de , si est une primitive de 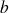, alors les solutions sont de la forme .

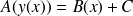Un cas particulier des équations différentielles à variables séparables est l'équation différentielle de la forme

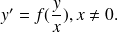
Pour se rendre compte que cette équation se ramène à une équation à variables séparables, il faut faire un changement de fonction inconnue :

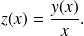
On obtient alors (le vérifier)

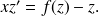
On peut alors avoir des solutions particulières constantes 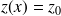(voir l'exercice référencé). Pour obtenir les autres solutions, on est ramené à résoudre l'équation différentielle à variables séparables

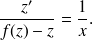
L'intégration de cette équation permet d'obtenir en fonction de 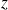. On obtient donc les solutions sous forme paramétrique, de paramètre