Soit l'oscillateur mécanique suivant
Étudier en fonction des valeurs de
 ,
,
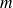 et
et
 le comportement de la solution de l'équation
le comportement de la solution de l'équation
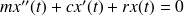 .
.
Quel est le comportement des solutions à l'infini ?
Aide simple
Les constantes
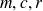 sont supposées positives. Plus précisément
sont supposées positives. Plus précisément
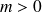 et on suppose qu'il y a au moins un ressort ou un piston, c'est à dire que l'on ne peut avoir
et on suppose qu'il y a au moins un ressort ou un piston, c'est à dire que l'on ne peut avoir
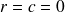 .
.
Etudier le signe du discriminant de l'équation caractéristique correspondante.
Aide simple
Solution : Le discriminant s'écrit
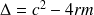 . On étudie alors les cas :
. On étudie alors les cas :
Regarder le signe des coefficients des exponentielles pour étudier le comportement à l'infini.
Aide simple
-
Si
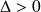 , les 2 racines de l'équation caractéristique sont négatives, car leur produit
, les 2 racines de l'équation caractéristique sont négatives, car leur produit
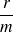 est positif et leur somme
est positif et leur somme
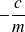 est négative, donc
est négative, donc
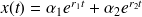 tend vers
tend vers
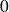 quand
quand
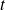 tend vers l'infini.
tend vers l'infini.
-
Si
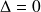 ,
,
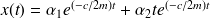 .
.
Si
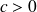 ,
,
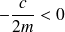 , donc là encore
, donc là encore
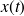 tend vers
tend vers
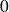 quand
quand
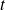 tend vers l'infini. Le cas
tend vers l'infini. Le cas
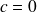 , n'est pas possible ici car
, n'est pas possible ici car
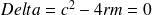 , il faudrait donc que
, il faudrait donc que
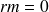 ce qui n'est pas possible (voir la première aide).
ce qui n'est pas possible (voir la première aide).
-
Si
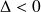 ,
,
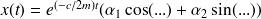 , si
, si
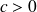 , comme précédemment
, comme précédemment
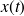 tend vers
tend vers
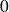 quand
quand
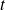 tend vers l'infini.
tend vers l'infini.
Par contre si
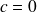 , ce qui est possible ici car
, ce qui est possible ici car
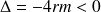 ,
,
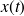 est une combinaison linéaire de sinus et cosinus, donc la solution oscille.
est une combinaison linéaire de sinus et cosinus, donc la solution oscille.
On retrouve un résultat bien connu, s'il y a frottement (
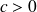 ), le mouvement est amorti et la solution tend vers l'état d'équilibre
), le mouvement est amorti et la solution tend vers l'état d'équilibre
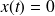 , s'il n'y a pas frottement (
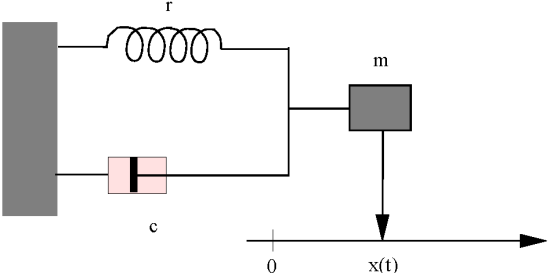
, s'il n'y a pas frottement (
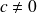 ), le mouvement est oscillant.
), le mouvement est oscillant.
 ,
,
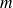 et
et
 le comportement de la solution de l'équation
le comportement de la solution de l'équation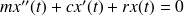 .
.
 ,
,
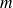 et
et
 le comportement de la solution de l'équation
le comportement de la solution de l'équation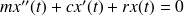 .
.