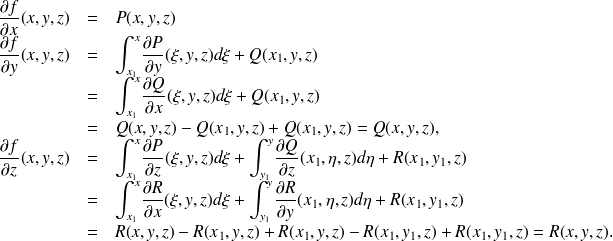On va démontrer le théorème suivant :
Soit
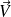un champ de vecteurs défini sur
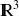dont les composantes
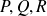admettent des dérivées partielles premiéres continues, supposons que
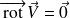, alors il existe une fonction
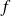qui vérifie
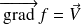
Puisque
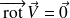, on a :
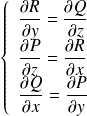
Soient
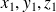des constantes, on définit la fonction
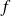de la fa\c{c}on suivante :
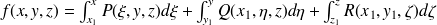
La fonction
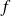est bien définie en effet puique
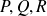ont des dérivées partielles premières continues, elles sont différentiables donc continues donc leurs applications partielles sont continues, chacune des intégrales est donc définie. On peut remarquer que le premier terme de
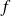dépend de
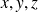, le deuxiéme terme de
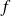dépend de
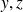, le troisième terme de
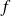dépend de
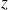.On obtient les dérivées partielles de
:
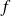