Soit
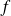une fonction de
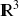dans
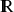dont les dérivées secondes sont continues, alors
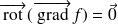
Démontrer ce théorème en exercice.
On va maintenant énoncer la réciproque du théorème précédent.
Soit
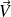un champ de vecteurs défini sur
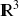dont les composantes
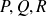admettent des dérivées partielles premières continues, supposons que le rotationnel de
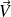soit nul, alors il existe une fonction
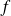, définie à une constante additive près, qui vérifie
.
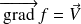On dit alors que le champ
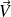dérive du potentiel scalaire
.
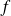Vous pouvez lire en document la démonstration de l'existence d'une fonction
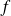qui vérifie
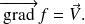
Supposons que
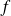et
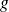sont 2 fonctions différentiables qui vérifient
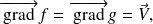
on montre en exercice que
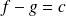où
est une constante.
Pour le calcul du potentiel, aller consulter l'exemple proposé.