L'influence de la mutation

Dans une population, l'ensemble des mutations ne modifie que très peu la composition allélique (quantitativement) mais introduit de nouvelles potentialités. Pour le démontrer, prenons une situation simple :

Soit un locus à deux allèles a1 et a2 :

A la génération n :

  • f(a1) = p

  • f(a2) = q

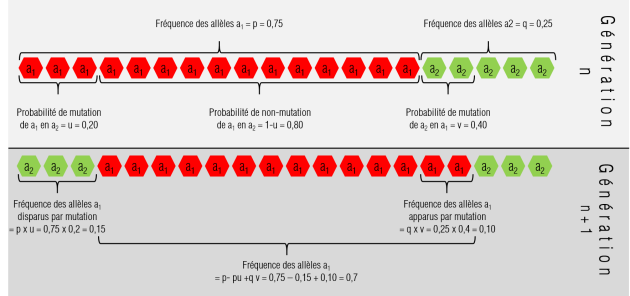
La probabilité de mutation de a1 vers a2 par génération et par gamète est appelée "u" (fig. 3.57).

La probabilité de mutation de a2 vers a1 par génération et par gamète est appelée "v" (fig. 3.57).

figure 3.57 : taux de mutations réciproques

Si en première approximation, u et v peuvent être considérées comme constantes, les fréquences p et q, elles, vont varier au cours des générations sous l'effet de la mutation.

A la génération n+1 :

  • f(a1) = p'

  • f(a2) = q'

Δp est alors la variation de p entre la génération n et la génération n+1

=> Δp = p'-p => p' = p + Δp

A cette génération n+1, nous allons trouver deux types d'allèles a1 :

  • ceux déjà présents à la génération n qui ne se sont pas transformés sous l'effet de la mutation

  • ceux qui proviennent de la transformation des allèles a2

Combien d'allèles a1 sont-ils devenus des allèles a2 ?

  • f(a1→a2) = fréquence des allèles a1 x probabilité de mutation a1 vers a2 = p x u

Combien d'allèles a2 sont-ils devenus des allèles a1 ?

  • f(a2→a1) = fréquence des allèles a2 x probabilité de mutation a2 vers a1 = q x v

Finalement, les allèles a1 de la génération n+1 sont ceux qui étaient présents en génération n (p) moins ceux qui ont été transformés en a2 (pu) mais plus ceux qui viennent de la mutation des allèles a2 (qv) :

  • p'= p-pu +qv (fig. 3.58)

figure 3.58 : Effets de la mutation sur la fréquence des allèles (attention : les fréquences de mutations u et v n'ont ici aucun rapport avec les fréquences réelles enregistrables, elles ne sont données que pour illustrer la démonstration.) Informations[1]

Puisque q = 1 - p, on en déduit :

  • p' = p –pu +(1-p)v = p-pu +v –pv = p +v -p(u+v)

  • p'-p =v-p(u+v)

En se rappelant que p'-p = Δp on en déduit :

  • Δp = v – p(u+v)

Un équilibre est atteint quand Δp = 0 c'est-à-dire quand autant d'allèles a1 sont transformés en allèle a2 que d'allèles a2 sont transformés en allèle a1 entre deux générations. Cherchons la fréquence peq à laquelle cet équilibre est atteint :

  • Δp = 0 => v – peq(u+v) = 0 => peq = v/(u+v)

A quelle vitesse va-t-on vers cet équilibre ?

Pour plus de simplicité, prenons une situation particulière : nous sommes à 0,1 de l'équilibre soit p - peq = 0,1

  • peq = v/(u+v) d'où v = peq(u+v)

remplaçons v dans la formule du Δp :

  • => Δp = v – p(u+v) = peq(u+v) - p(u+v) = (p-peq)(u+v)

u et v ont pour ordre de grandeur 10-6 et p-peq= 0,1 = 10-1

Donc Δp # 10-7