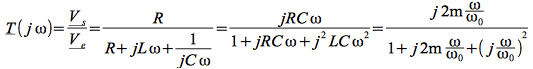Circuit RLC série
Le circuit RLC série s'obtient simplement en mettant en série, alimentés par la source sinusoïdale, les trois dipôles résistance, condensateur et solénoïde. Selon que la tension de sortie est prélevée sur la résistance, le condensateur ou le solénoïde, les résultats seront différents et on obtiendra respectivement un passe-bas, un passe-haut ou un passe-bande. On traitera dans ce paragraphe uniquement du passe-bande mais le lecteur est encouragé à traiter les deux autres cas avec le même schéma, soit : l'analyse théorique en écrivant la fonction de transfert complexe et en l'étudiant analytiquement, puis en la traçant avec Scilab puis en faisant des simulations PScipe du circuit correspondant.
Le lien ci-dessous permet télécharger le schéma PSpice du circuit RLC passe-bande.
Fonction de transfert
Par application de la structure du pont diviseur, on obtient aisément la fonction de transfert :
avec : 
et 
. On trouve aussi souvent dans la littérature le facteur de qualité défini par : 
Diagramme de Bode
On a pris les valeurs suivantes : 
et 
et 
donc
soit
et par ailleurs, 
soit 
On obtient alors le diagramme de Bode suivant :
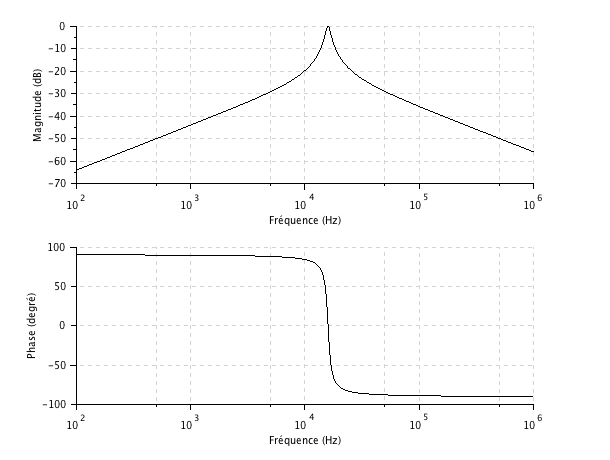
On découvre ici le phénomène de résonance : le gain est maximum à la pulsation
. A cette pulsation, l'impédance du circuit RLC série se réduit à la résistance du circuit
et ainsi l'impédance totale du dipôle RLC série s'écrit :
Le dipôle est alors réduit à une résistance et on montre aisément que le gain est maximal dans cette condition. Par ailleurs, on voit sur le diagramme de phase, qu'à cette pulsation, le déphasage est nul. On constate que lorsque la pulsation tend vers 0, le gain tend vers 0 et la phase vers 90° tandis que lorsque la pulsation tend vers l'infini, le gain tend aussi vers 0 et la phase vers -90°. On peut lire encore sur le diagramme de gain que la décroissance pour les fréquences basses et hautes se fait au rythme de -20 dB par décade.
Le circuit est un filtre passe-bande qui laisse passer les fréquences autour de sa fréquence de résonance : la bande passante est définie par les deux valeurs de fréquence (
) autour de la résonance pour lesquelles le gain vaut -3 dB par rapport au gain à la résonance, ici 0 dB. On montre aisément que la bande passante en fréquence du filtre est directement liée à son facteur de qualité par la formule :
Il est aisé de modifier les valeurs de composants avec Scilab pour obtenir rapidement le diagramme de Bode correspondant : ci-après, le diagramme de Bode pour une résistance dix fois moindre soit : 
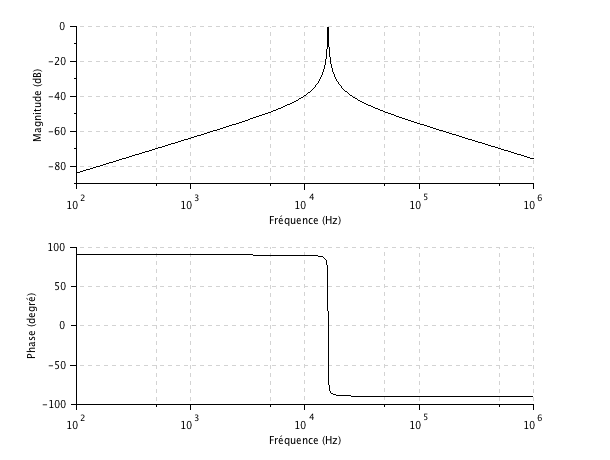
où l'on voit que le pic de résonance est maintenant beaucoup plus fin : on dira qu'un tel filtre est très sélectif puisqu'il ne laisse passer qu'une fine bande de fréquences autour de la fréquence de résonance. Les autres caractéristiques du filtre, savoir, les phases et les décroissances du gain pour les fréquences basses et hautes sont inchangées. Inversement lorsque le facteur de qualité diminue, l'acuité du pic de résonance diminue également jusqu'à disparaître. A la limite, quand le facteur de qualité est suffisamment faible, d'un point de vue formel, le dénominateur se factorise et le filtre devient équivalent au produit de deux fonctions de transfert du premier ordre.
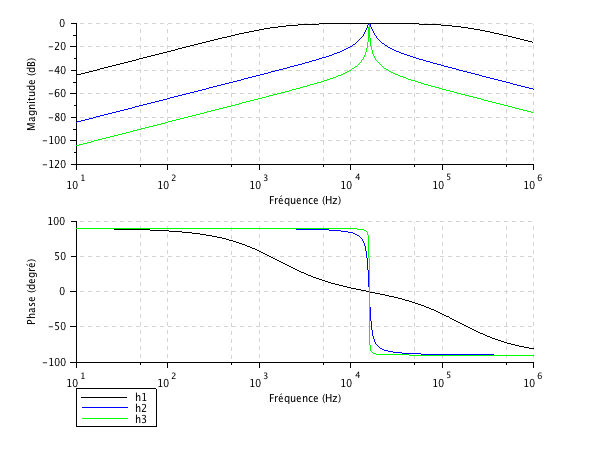
La figure ci-dessous représente les trois fonctions de transfert avec les composants suivants : 
et 
donc 
soit 
et par ailleurs, 
soit 
(h3) ; 
soit 
(h2) ; 
soit 
(h1).
