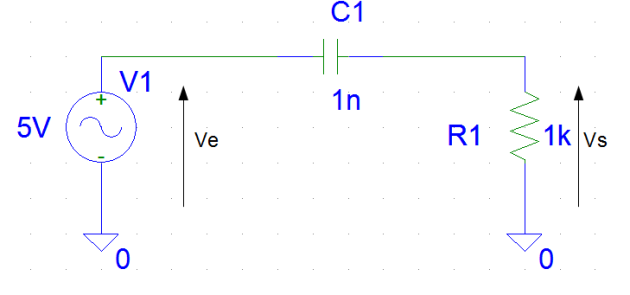
Circuit RC
Le circuit RC ci-dessous est le circuit le plus simple qu'on puisse envisager pour présenter la problématique du filtrage analogique. Il convient d'introduire la notion de fonction de transfert.
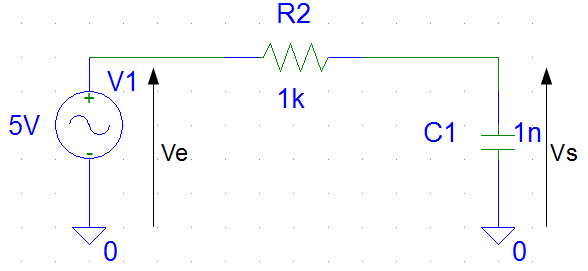
Fonction de transfert
En considérant le circuit comme un système avec une entrée et une sortie, à savoir les tensions nommées respectivement Ve et Vs, on définit la fonction de transfert comme le rapport des tensions en représentation complexe :
.
Cette fonction de transfert est donc un complexe qui prend une valeur a priori différente pour chaque valeur de pulsation de la tension d'alimentation, ici Ve .
On obtient aisément cette fonction de transfert en reconnaissant la structure d'un pont diviseur :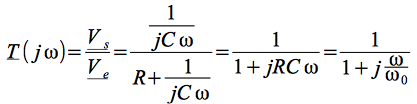
avec
en 
.
Le lien ci-dessous permet de télécharger le schéma PSpice du circuit RC précédent :
Diagramme de Bode
Le diagramme de Bode consiste simplement en une représentation graphique de la fonction de transfert en fonction de la pulsation. Différentes formes de telles représentations graphiques existent. Le diagramme de Bode est la plus naturelle : il consiste à tracer dans deux diagrammes respectivement le module et l'argument de la fonction de transfert complexe en fonction de la pulsation placée sur l'axe des abscisses. Plus précisément, on trace 
en fonction de la pulsation d'une part et 
en fonction de la pulsation, d'autre part. Le diagramme de Bode consiste donc en fait en deux diagrammes, un pour le module et l'autre pour la phase qu'on a tendance à oublier mais qui est une information importante également. Qui plus est, l'axe des abscisses est généralement représenté en échelle log de manière à représenter une dynamique importante, c'est à dire une variation de fréquence sur une plage importante. Chaque graduation correspond à une multiplication par 10 de la pulsation (ou fréquence).
Dans le cas général, une fonction de transfert se présente comme un rapport de deux complexes puisqu'elle représente la sortie divisée par l'entrée. Le numérateur (respectivement le dénominateur) peut encore se décomposer en un produit de facteurs. Amplitude ou module d'une part, et argument ou phase d'autre part sont déterminés depuis la fonction de transfert complexe comme classiquement pour n'importe quel nombre complexe comme suit : le module d'un produit (respectivement d'un rapport) est le produit (respectivement le rapport) des modules et l'argument d'un produit (respectivement d'un rapport) est la somme (respectivement la différence) des arguments.
On peut se demander pourquoi on a choisi de représenter
. Il y a une raison et il importe de la connaître. Lorsque 
, 
et partant, 
(le dB est l'unité décibel). Cette situation correspond au fait que tension de sortie et tension d'entrée sont dans le rapport 
. Comme la puissance est proportionnelle au carré de la tension, la situation correspond à un rapport ½ entre puissance de sortie et puissance d'entrée. On retiendra qu'on identifiera souvent sur le diagramme de Bode en module, la fréquence ou pulsation pour laquelle le gain, savoir 
, vaut -3 dB par rapport au gain pour la fréquence nulle.
Si on revient à la fonction de transfert du schéma ci-dessus, 
, on peut regarder les valeurs limites quand la pulsation prend des valeurs extrêmes. En l'occurrence, lorsqu'on fait tendre la pulsation vers 0, la fonction de transfert tend vers 1, soit 
. Il s'agit là du gain dit statique (pulsation nulle correspond à une tension continue). La tension de sortie tend vers la tension d'entrée. Quand la pulsation tend vers l'infini, au dénominateur de 
, 1 devient négligeable devant 
et 
tend vers 0, et partant
, tend vers moins l'infini. A la pulsation 
telle que 
soit
, on a le fameux
. Il faut encore constater que lorsque la pulsation tend vers l'infini, la décroissance du gain devient asymptotiquement linéaire avec une pente de -20 dB par décade ; quand la pulsation passe d'une valeur à 10 fois plus (une décade), le gain a perdu 20 dB. On voit tout ça sur le diagramme de Bode tracé avec Scilab.
Exemple :
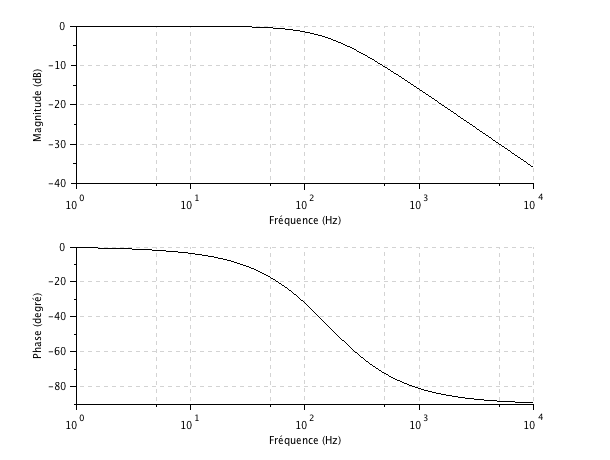
Dans cet exemple, on a choisi 
et 
donc
soit 
à l'arrondi près. On voit, à cette fréquence, les valeurs caractéristiques pour un passe-bas du premier ordre, le gain à -3dB par rapport à la fréquence nulle et le déphasage à 45°.
On peut à présent tracer le diagramme de Bode du filtre passe-haut du premier ordre qui est obtenu simplement en échangeant résistance et condensateur selon la figure ci-dessous :
On obtient aisément cette fonction de transfert en reconnaissant là encore la structure d'un pont diviseur :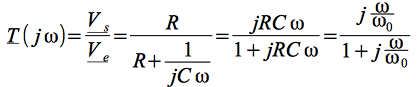
avec, comme précédemment 
, en
On en trace la fonction de transfert avec
et 
donc
.
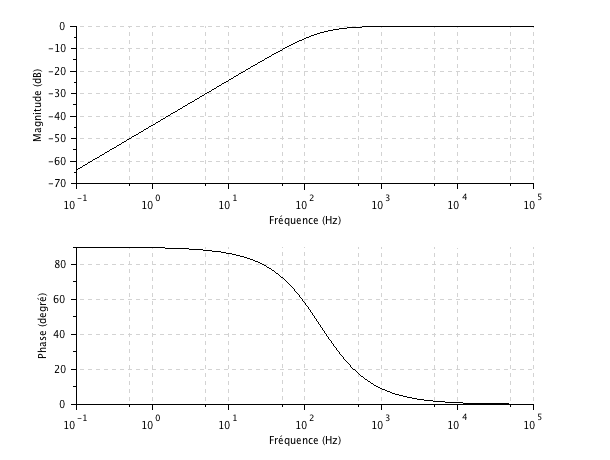
Là encore, on reconnaît les éléments caractéristiques du filtre passe-bas du premier ordre, la fréquence dite de coupure à -3 dB, ici à 159 Hz environ, fréquence pour laquelle on obtient un déphasage de 45°.
Le lien ci-dessous permet de télécharger le schéma PSpice du circuit RC passe-haut.
Remarque :
Il existe une astuce pour reconnaître le caractère passe-bas ou passe-haut d'un circuit quelconque du premier ordre dans lequel on a associé plusieurs résistances et plusieurs condensateurs. Quand la fréquence tend vers 0 (régime continu), le condensateur se comporte comme un circuit ouvert tandis que lorsque la fréquence tend vers l'infini, le condensateur se comporte comme un court-circuit. En faisant une analyse simple en remplaçant respectivement le condensateur par un circuit ouvert ou un court-circuit, on voit souvent quasi instantanément si la tension de sortie tend vers 0 ou vers la tension d'entrée. Évidemment, si on dispose de la fonction de transfert, il suffit de faire tendre la fréquence vers 0 puis vers l'infini pour en déduire le comportement et par voie de conséquence, la nature passe-bas ou passe-haut du filtre correspondant.
