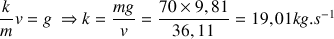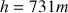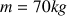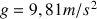Le saut sans parachute
Le 23 mai 2012, le cascadeur britannique Gary Connery a sauté depuis un hélicoptère d'une hauteur
|  |
Question
On considère, dans un premier temps, qu'il n'avait pas de combinaison ailée et que l'on néglige totalement les frottements de l'air.
a) Donnez l'équation horaire de la trajectoire
.
a) Le système étudié ici est le cascadeur (repérée par son centre d'inertie G). Pour faire l'étude de son mouvement on choisit de prendre un référentiel terrestre (supposé galiléen).
Les forces qui agissent sur le système sont :
- le poids
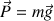
- les frottements de l'air, mais qui sont négligés dans cette partie.
Il s'agit donc d'un mouvement de chute libre.
On applique la 2ème loi de Newton sur le système :
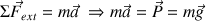
Le texte indique que le mouvement de chute est rectiligne vertical suivant un axe
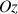dirigé vers le bas. On a la situation suivante :
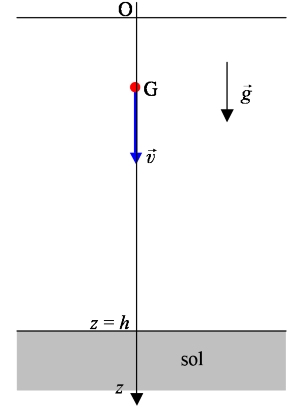
Dans ces conditions le vecteur accélération de la pesanteur est dirigé vers le bas, dans le sens positif de l'axe vertical
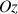. Le vecteur accélération
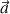du centre d'inertie du cascadeur est donc :
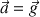
La projection sur l'axe
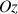donne :
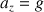
Le vecteur accélération correspond à la variation du vecteur vitesse :
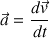
Le mouvement étant vertical, il n'y a que la composante suivant
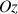qui est non nulle :
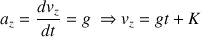
On doit évaluer la constante d'intégration
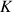. Les coordonnées du vecteur vitesse doivent être exactes même pour
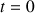. D'après la relation ci-dessus, on a
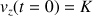. Or le cascadeur saute de l'hélicoptère sans vitesse initiale, c'est-à-dire avec
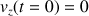. La constante est donc nulle. La vitesse du cascadeur est donnée par :
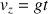
Le vecteur vitesse correspond à la variation du vecteur position :
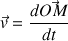
Ici aussi, seule la composante verticale est non nulle :
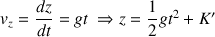
On doit évaluer la constante d'intégration
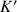. Les coordonnées du vecteur position doivent être exactes même pour
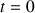. D'après la relation ci-dessus, on a
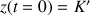Or le cascadeur saute de l'hélicoptère à la position repérée par
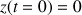. La constante est donc nulle. La position du cascadeur est donnée par :
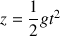
L'équation horaire de la trajectoire est :
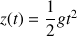
que l'on peut aussi écrire :
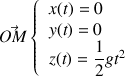
Question
b) Quelle aurait été la durée de la chute ?
b) D'après l'équation horaire de la trajectoire :
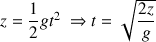
La chute est de
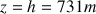. Soit un temps de chute
:
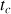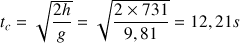
Question
c) Quelle aurait été la vitesse à son atterrissage ? Donnez cette vitesse en
.
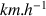c) D'après l'équation horaire de la vitesse, au bout du temps
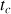, la vitesse d'atterrissage est :
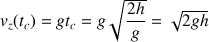
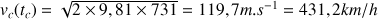
Question
d) Retrouvez ce résultat, en utilisant un calcul d'énergie.
d) Comme dans cette partie on ne considère pas les frottements, l'énergie mécanique (ou énergie totale) du cascadeur se conserve au cours de la chute. Donc il n'y a pas de variation d'énergie :
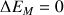. La variation d'énergie mécanique est reliée aux variations d'énergie cinétique et d'énergie potentielle. On a ainsi :
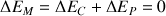
La variation d'énergie cinétique est :
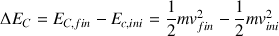
Ici
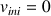, soit :
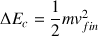
Par définition, la variation d'énergie potentielle est reliée à l'opposé du travail des forces :
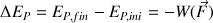
Ici la seule force est la force de poids
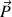. Le travail s'écrit
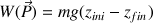. Or si la force qui crée le mouvement est dans le même sens que le déplacement, le travail est moteur et est positif. On doit avoir
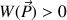, ce qui impose
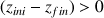. On doit donc considérer une différence d'altitude positive, soit
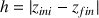. Dans ces conditions, la variation d'énergie potentielle s'écrit :
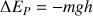
La variation d'énergie mécanique est donc donnée par :
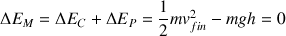
La vitesse finale est :
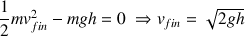
On retrouve bien la forme de la vitesse de la question 1. c)
Attention. L'application directe de la formule de l'énergie mécanique peut apporter des erreurs de calcul si on ne tient pas compte que la variation de l'énergie potentielle est négative. En effet, le travail de la force est positif, c'est un travail moteur, mais la variation d'énergie potentielle est négative, c'est l'opposée du travail.
Question
Pour aller un peu plus loin, on considère maintenant qu'il avait sa combinaison ailée. Lors de sa chute, il subit une force de frottement de l'air. Cette force s'oppose au mouvement et est proportionnelle à la vitesse de chute : sa forme mathématique s'écrit
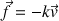, où
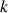est le coefficient de frottement.
a) Faites l'étude du système. Donnez les expressions du vecteur accélération
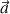et de l'accélération
.
a) On refait l'étude du système, donc ici est le cascadeur (repérée par son centre d'inertie G), mais en tenant compte des forces de frottement. On se place à nouveau dans un référentiel terrestre (supposé galiléen).
Les forces qui agissent sur le système sont maintenant :
- le poids
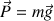
- les frottements de l'air
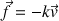
Il ne s'agit donc plus d'un mouvement de chute libre.
On applique la 2ème loi de Newton sur le système :
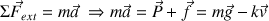
Le vecteur accélération est alors :
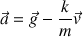
La projection de ce vecteur sur l'axe vertical
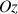, dirigé vers le bas, donne :
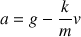
Question
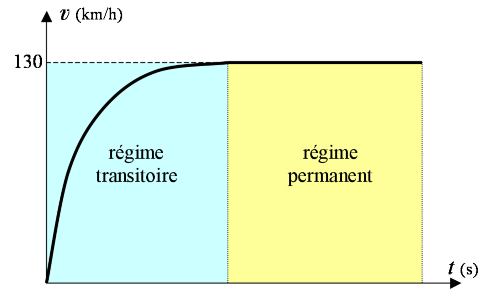
b) Peu après son saut, sa vitesse s'est stabilisée à 130 km/h . Faites un schéma représentant la vitesse en fonction du temps et définissez sur ce schéma les deux régimes de descente : le régime transitoire et le régime permanent.
b) Le cascadeur débute sa chute sans vitesse initiale. Au cours de la chute, sa vitesse va croître : c'est le régime transitoire. Mais plus la vitesse du cascadeur augmente, plus les forces de frottement augmente, puisqu'elles sont proportionnelles à la vitesse. Donc, plus il va vite plus sa vitesse augmente lentement. Et ce jusqu'à ce que le terme des forces de frottement
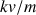devienne identique à l'accélération de la pesanteur
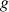. L'accélération est alors nulle : c'est le régime permanent. On a schématiquement :
Question
c) Écrivez l'équation différentielle de la vitesse et calculez le coefficient de frottement
c) L'équation différentielle de la vitesse s'obtient en partant du fait que l'accélération correspond aux variations de la vitesse, soit :
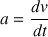
Ce qui donne :
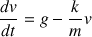
On écrit l'équation différentielle de la vitesse sous la forme :
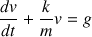
Le coefficient de frottement est une constante pendant tout le mouvement. On peut donc le déterminer en régime transitoire (calcul compliqué) ou en régime permanent (calcul plus simple).
En régime permanent, la vitesse
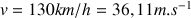est constante, donc
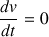. Ainsi le coefficient de frottement
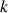est :
