Mouvement du centre d'inertie d'un solide
Pour éprouver sa force, un joueur dispose d'une piste sur laquelle il propulse puis abandonne un palet de masse
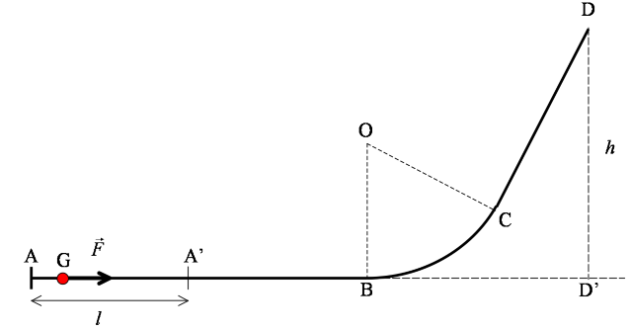
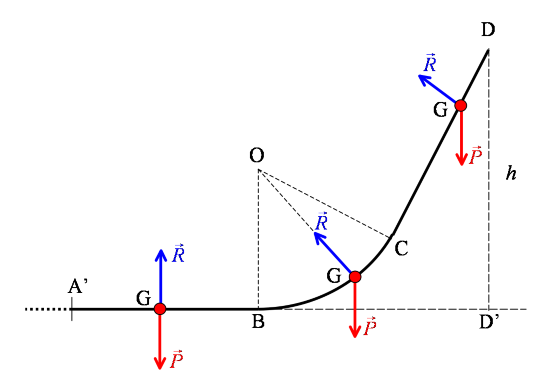
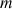. La piste située dans un plan vertical est formée d'une partie rectiligne horizontale (AB), raccordée tangentiellement à un arc de cercle (BC), raccordé lui-même à une partie rectiligne inclinée (CD). Le schéma ci-dessous représente la trajectoire suivie par le centre d'inertie G du palet. L'épreuve est réussie si G parvient en D, à une hauteur
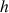au-dessus du plan horizontal qui contient AB. Les frottements sont négligés.
Une force de propulsion
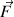, constante, d'intensité
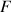, est exercée sur le palet tout le long du trajet
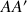de longueur
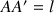. Cette force cesse en
.
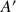Données :
Accélération de la pesanteur :
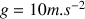
Longueur de lancement :
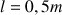
Hauteur du point D :
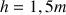
Masse du palet :
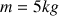
Question
Sur un schéma, représentez la force de propulsion
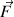, la force de poids du palet
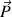et la force de réaction de la piste sur le palet
.
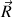La force de propulsion
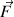est horizontale dirigée dans le sens du mouvement et appliquée au centre de gravité
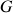. La force de poids du palet
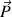est toujours verticale dirigée vers le bas et appliquée au centre de gravité
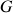. La force de réaction de la piste sur le palet
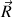est toujours perpendiculaire au point de contact du palet avec la piste, soit ici verticale dirigée vers le haut et appliquée au point de contact. Ces forces sont schématisées comme suivant :
Question
Rappeler la relation qui lie la variation d'énergie cinétique au travail des forces.
La relation qui lie la variation d'énergie cinétique
(entre l'énergie cinétique finale
et l'énergie cinétique initiale
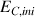au travail des forces extérieures (ou plus généralement à la somme des travaux des forces extérieures) s'écrit :
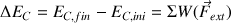
Question
Durant le trajet
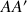, parmi les trois forces qui agissent sur le palet, quelles sont celles dont le travail n'est pas nul. Expliquer pourquoi. Si le travail d'une force n'est pas nulle, précisez si ce travail est moteur ou résistant ?
Pour une force
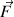constante dont le point d'application se déplace de
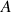à
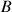et dont sa direction fait un angle
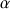avec la direction du vecteur
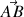selon le schéma suivant :
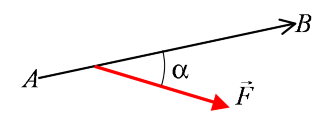
alors le travail
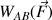est égal au produit scalaire du vecteur
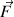par le vecteur
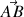. Cette relation s'écrit :
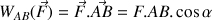
Ainsi, si l'angle
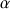vaut
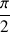(ou 90°), le travail de la force est nul. Donc le travail d'une force qui s'exerce perpendiculairement au déplacement est nul.
Pour le problème proposé les forces de poids
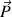et de réaction du support
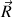sont perpendiculaires au déplacement
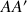; leurs travaux sont nuls :
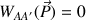et
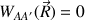
La force de propulsion
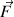fait un angle
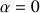avec la direction de déplacement
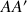; son travail vaut :
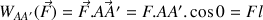
Comme la force de propulsion
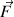est dirigée dans le sens du déplacement, le travail est moteur. On remarque d'ailleurs que son expression
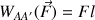est positive.
Question
Soit
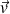la vitesse du centre d'inertie
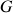du palet en
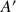. En appliquant le théorème de l'énergie cinétique (relation de la question 2), exprimer la valeur
de la vitesse de
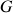en
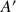en fonction de
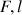et
.
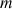Le théorème de l'énergie cinétique s'écrit :
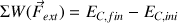
soit :
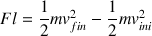
Le palet part de
à l'instant initial avec une vitesse
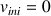et arrive en
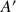à l'instant final avec la vitesse
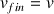; on a alors :
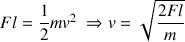
Question
Durant le trajet
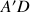, parmi les deux forces qui agissent sur le palet (la force de propulsion cesse en
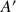), quelles sont celles dont le travail n'est pas nul. Expliquer pourquoi. Si le travail d'une force n'est pas nulle, précisez si ce travail est moteur ou résistant ?
On se trouve dans la situation où la force de propulsion
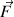a cessée. La force de poids du palet
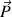est toujours verticale dirigée vers le bas et appliquée au centre de gravité
. La force de réaction de la piste sur le palet
est toujours perpendiculaire au point de contact du palet avec la piste et appliquée au point de contact, mais sa direction varie avec la courbure de la piste. On peut schématiser ces forces à différents moments comme suivant :
Durant le trajet
, la force de réaction du support
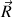est toujours perpendiculaire au
déplacement ; son travail est nul :
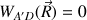
Par contre, la force de poids
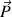est toujours verticale. Durant le trajet
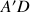, l'orientation de la force
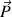par rapport à la direction du déplacement varie. Durant le trajet
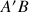, la force
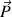est perpendiculaire au déplacement et son travail est nul. Mais durant le trajet
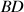, la direction de la force
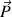fait un angle
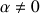par rapport au vecteur déplacement. Son travail n'est pas nul. Ainsi :
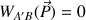
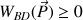
De plus, on remarque que sur tout le trajet
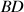, l'angle entre la direction de la force de poids et la direction du déplacement est
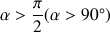. Le cosinus de cet angle est négatif et le travail est négatif : le travail du poids sur le déplacement
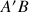est nul, mais est négatif, donc résistant sur le trajet
.
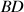Question
Soit
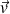la vitesse du centre d'inertie
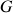du palet en
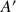. En appliquant le théorème de l'énergie cinétique (relation de la question 2), exprimer
en fonction de
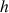pour que G atteigne
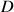avec une vitesse nulle.
Le théorème de l'énergie cinétique s'écrit toujours :
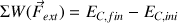
Le palet part de
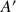avec une vitesse
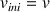et doit arriver en D avec la vitesse
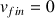; on a alors :
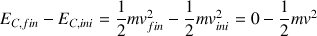
Le travail de la force de poids est un travail résistant. La hauteur
d'ascension étant petite, on considère qu'il n'y a pas de variation de l'accélération de la pesanteur sur le trajet. La force de poids est ainsi conservative et son travail ne dépend pas du trajet suivi. Le travail de la force de poids est identique au travail (résistant) pour monter le palet d'une hauteur
, soit :
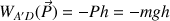
On a ainsi :
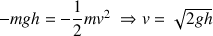
Question
Déduire des questions 4 et 6 l'intensité
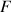de la force de propulsion qui permet à
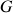d'arriver en
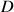avec une vitesse nulle. On exprimera
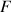en fonction de
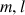et
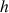. Puis calculer la valeur numérique de
.
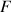Dans les questions 4 et 6, on a calculé dans les deux cas la vitesse
en
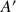en fonction de la force de propulsion (question 4) et pour que le palet arrive en D avec une vitesse nulle (question 6). On a donc :
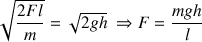
La valeur numérique de
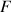vaut :
