Conductivité d'une solution
On dissout 0,5 g de nitrate de calcium Ca(NO3)2 dans une fiole jaugée de 200 mL.
Données : masse molaire :
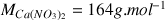
Conductivités molaires à 25°C :
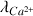= 11,90 mS m² mol-1 ;
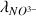= 7,14 mS m2 mol-1
Conductivités molaires à 20°C :
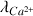= 7,44 mS m2 mol-1 ;
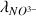= 6,43 mS m2
Question
a) Indiquer les ions présents en solution et calculer leurs concentrations.
Ca(NO3)2 → Ca2+(aq) + 2 NO3-(aq)
On va considérer que la concentration apportée en Ca(NO3)2 est c
=
×
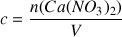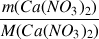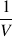avec n(Ca(NO3)2) =
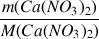
A.N. c =
×
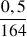D'après l'équation de dissolution de Ca(NO3)2 on a :
[Ca2+] = c et [NO3-] = 2c
On peut utiliser un tableau d'avancement simplifié pour établir ces relations :
Ca(NO3)2 → Ca2+(aq) + 2 NO3-(aq) | ||
|---|---|---|
n0 = c.V | 0 | 0 |
0 | c.V | 2×c.V |
Donc après dissolution
nombre de mole de Ca2+ : n(Ca2+) = c.V et [Ca2+] =
=
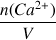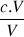= c
nombre de mole de NO3- : n(NO3-) = 2×c.V et [NO3-] =
=
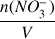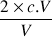= 2c
D'où
[Ca2+] = 0,0152 mol.L-1 et [NO3-] = 0,0305 mol.L-1
Question
b) Calculer la conductivité
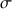à 25 °C et 20°C. Expliquer la différence de résultat.
Données : masse molaire :
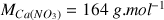
Conductivités molaires à 25°C :
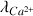= 11,90 mS m2 mol-1 ;
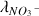= 7,14 mS m2 mol-1
Conductivités molaires à 20°C :
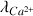= 7,44 mS m2 mol-1 ;
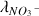= 6,43 mS m2
A 25°C
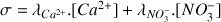
d'où
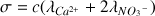
Attention il faut utiliser les concentrations en mol.m-3 et pas en mol.L-1 !
[Ca2+] = c = 15,2 mol.m-3 (donc [NO3-] = 30,5 mol.m-3
A.N.
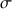= 15,2×(11,90 + 2×7,14)
unité : mol.m-3 × mS.m2.mol-1 = mS.m-1
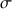= 398 mS.m-1 à 25 °C
A 20°C
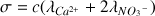
A.N.
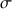= 15,2×(7,44 + 2×6,43)
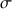= 309 mS.m-1 à 20 °C
On constate que la conductivité
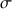d'une solution dépend fortement de la température. Plus la température augmente, plus la mobilité des ions augmente (ce qui entraîne une augmentation de
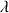) et donc plus la conductivité augmente.
