Tables des lois d'addition et de multiplication modulo p
En plus des groupes infinis comme
,
,
,
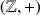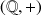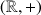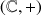, ou encore
,
,
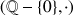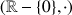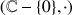, il y a aussi des groupes qui n'ont qu'un nombre fini d'éléments. Une classe intéressante d'exemples de cette forme s'obtient en considérant les calculs usuels dans les entiers
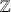modulo un entier
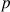, c'est-à-dire qu'on ne retient du résultat de l'opération que le reste dans la division entière par
.
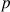On obtient ainsi l'ensemble
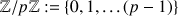
aussi noté
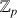,muni des deux lois de composition interne
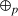et
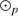définies comme l'addition et la multiplication usuelle modulo
:
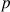L'appliquette ci-dessous permet de visualiser les tables de ces lois pour différentes valeurs de
:
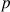On observe que pour toutes les valeurs de
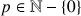la loi d'addition munit
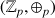d'une structure de groupe: toute ligne et toute colonne est une permutation de l'ensemble, en particulier l'élément neutre de l'addition,
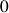, apparaît une et une seule fois. Chaque colonne est la même que la précédente mais décalée cycliquement d'un cran, on dit que le groupe est cyclique. Les valeurs le long des diagonales Sud-Ouest/Nord-Est sont constantes.
Par contre, la loi de multiplication ne munit pas toujours
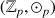d'une structure de groupe, même en éliminant la ligne et la colonne
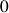. C'est le cas uniquement quand l'entier
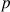est un nombre premier. On observe en effet que si
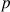n'est pas premier, des
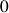apparaissent dans les lignes et les colonnes de ses diviseurs, et l'élément neutre de la multiplication,
, n'apparaît pas dans ces colonnes là.
