Propriétés de la transformation de Fourier
Nous allons les étudier, au moins certaines d'entre elles sur l'intégrale de Fourier, c'est-à-dire pour les fonctions de
bien qu'aujourd'hui, la transformée de Fourier discrète est a priori plus importante puisque les signaux sont massivement numérisés. Néanmoins, les propriétés que nous verrons sont valables aussi bien pour l'intégrale de Fourier que pour la transformée discrète et peut-être un peu plus facile à établir dans le cas de l'intégrale. Nous ne démontrerons pas toutes les nombreuses propriétés, ce n'est pas le but de ce cours, ni n'insisterons beaucoup sur la théorie qui les fondent. Nous souhaitons plutôt montrer en quoi une connaissance raisonnable de ces propriétés est utile pour lire et interpréter les calculs que sortent maintenant les ordinateurs ou oscilloscopes numériques qui sont pourvus de modules « transformée de Fourier ». Pour une liste exhaustive de propriétés, il faut se reporter à un ouvrage ou à un formulaire. Nous démontrerons les premières propriétés pour comprendre la logique de la preuve ce qui aide à l'appropriation du concept. Ensuite, nous considérerons que le lecteur sera capable d'établir lui-même les démonstrations parce qu'elle seront de difficulté et de technique très comparable et nous nous contenterons alors de donner les résultats sans démonstration.
On utilisera les notations suivantes (valables aussi pour les chapitres suivants) :
désigne le complexe conjugué de 
Le signal 
étant issu d'un processus physique, il sera sauf extraordinaire, considéré comme étant réel. Sur le plan le plus général, on peut aussi l'envisager comme étant un signal complexe. Nous le ferons pour l'une ou l'autre propriété.
Linéarité
Soient,
et 
deux fonctions de 
, 
et 
de 
, on démontre aisément que :
Translation temporelle
Le signal temporel translaté de
s'écrit 
.
Par changement de variable 
,soit 
, l'expression devient :
On reconnaît en effet dans la dernière intégrale, l'intégrale de Fourier mais écrite en variable u. Cette variable est toutefois une variable muette, homogène à un temps.
On constate que la translation temporelle dans l'espace direct correspond à une multiplication par 
dans l'espace réciproque. Or cette multiplication par ce facteur correspond à une modulation par la fréquence 
puisque l'exponentielle complexe équivaut à une fonction trigonométrique.
Modulation temporelle
La propriété précédente appelle directement la suivante. Que se passe-t-il si on module en amplitude mais dans l'espace direct ?
La modulation en amplitude dans l'espace direct à la fréquence 
, se traduit dans l'espace réciproque, par la translation par.
Dérivation dans l'espace direct
par intégration par parties, soit :
Le premier terme est nul parce que 
étant une fonction de 
, elle tend vers 0 quand t tend vers les deux infinis.On admet (ou on démontrera à titre d'exercice) la généralisation à la dérivée temporelle d'ordre n :
On constate que la dérivation dans l'espace direct se traduit par la multiplication par 
pour chaque ordre de dérivation dans l'espace réciproque. C'est un résultat crucial : dériver peut donner lieu à des calculs difficiles. Dans l'espace réciproque, l'opération complexe de dérivation se traduit par une simple multiplication. Ce résultat nous rappelle quelque chose : la relation tension – courant aux bornes d'un solénoïde s'écrit :
et se traduit dans le cas du régime permanent en notation complexe par : 
. Le résultat est tout à fait équivalent : la dérivation dans les valeurs instantanées se traduit par la multiplication par 
. C'est évidemment lié aux propriétés des exponentielles complexes qui en font des objets mathématiques particulièrement commodes.
Dérivation dans l'espace réciproque
En calculant 
de manière tout à fait analogue, on obtient une formule comparable dont on admet la généralisation à l'ordre n :
La dérivation dans l'espace réciproque se traduit par la multiplication par 
pour chaque ordre de dérivation dans l'espace direct.
Remarque :
Les deux définitions intégrales de Fourier directe et inverse et les premières propriétés démontrées dans les lignes précédentes montrent à quel point les relations sont symétriques. Les mathématiciens parlent pour espace temporel et fréquentiel ou plus généralement espace direct et fréquentiel, d'espaces duals.
Changement d'échelle
avec le changement de variable
.Il y a dans la suite de la démonstration la petite subtilité suivante : il faut distinguer les deux cas, a positif et a négatif (a est évidemment non nul).Si a est positif, les bornes d'intégration implicites ne sont pas changées, par contre si a est négatif, moins l'infini devient plus l'infini et réciproquement : il y a un signe moins qui apparaît à cause du retournement des bornes. On peut toutefois synthétiser facilement les deux cas par la formule unique suivante et nous laissons le soin au lecteur qu'elle est bien conforme aux deux cas (a positif et a négatif) :
Diverses propriétés
Pour comprendre la logique de la preuve, nous calculons :
La question est la suivante : puisque t est transformé en -t, le facteur
doit-il être transformé en 
dans l'intégrale ? La réponse est non. Il ne faut pas oublier la signification de la transformée en tant que changement de base : calculer la transformée de Fourier, c'est projeter le signal sur les exponentielles complexes, c'est-à-dire calculer le produit scalaire, en l'occurrence :
On applique ensuite le changement de variable 
et il faut bien observer que ce changement de variable retourne les bornes implicites d'intégration. Mais comme 
, ce signe moins est compensé par celui qui résulte du retournement des bornes d'intégration. Finalement :
puisque l'intégrale de Fourier est celle de la transformée inverse avec u comme variable muette.
Remarque :
Pour le physicien, le signal de l'espace direct est un signal temporel et on calcule des transformées directes sur ces signaux temporels. De manière analogue, on calcule des transformées inverses de signaux fréquentiels. Dans la formule ci-dessus, le second membre représente la transformée inverse d'un signal temporel. Même si la signification physique de cette opération n'est pas évidente à percevoir, sur un plan théorique, rien n'empêche de le faire. Il faut juste comprendre que temps et fréquence sont des variables duales et que quelque transformée qu'on applique (directe ou inverse) sur un espace, on passe dans l'espace dual.
On admet sans démonstration les deux formules suivantes. On laisse au lecteur le soin de les démontrer moyennant une technique très similaire à la démonstration ci-dessus :
Enfin, nous admettons sans démonstration un groupe de propriétés relatives à des symétries qui apparaissent dès lors que les signaux sont réels ou imaginaires purs. On note dans ces formules,
, la partie réelle de 
et 
, la partie imaginaire de 
:
On a alors :
La deuxième équation est particulièrement importante et explique une observation que nous avons faite dans les manipulations Scilab. Quand le signal est réel (partie imaginaire nulle), on a immédiatement :
et partant l'égalité des modules, soit :
Le graphe du module de la transformée de Fourier d'un signal réel est ainsi pair. On observe une symétrie légèrement différente sur les signaux réels échantillonnés ci-dessous et le spectre du signal bleu (on obtiendrait quelque chose de très similaire sur le signal rouge). Il faut bien comprendre que dans la transformée de Fourier discrète, il n'y a pas de fréquence négative puisque les composantes fréquentielles sont indicés de 0 à N. En réalité, les N/2 premiers points correspondent aux fréquences positives de 0 à 
. Par contre, les N/2 points suivants (complémentaires à N) représentent en fait les fréquences négatives symétriques en l’occurrence sur le module de la transformée de Fourier aux fréquences positives. C'est ainsi que la parité dans les formules de l'intégrale de Fourier des fonctions de 
se traduit par la symétrie par rapport à l'axe vertical qui passe par N/2 dans les graphes de la transformée de Fourier discrète. Sans entrer dans les détails, cette correspondance est liée très directement à la périodicité des exponentielles échantillonnées, 
.
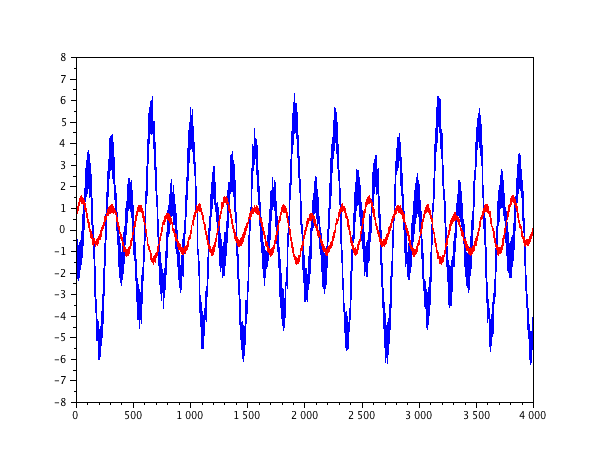
Deux signaux réels
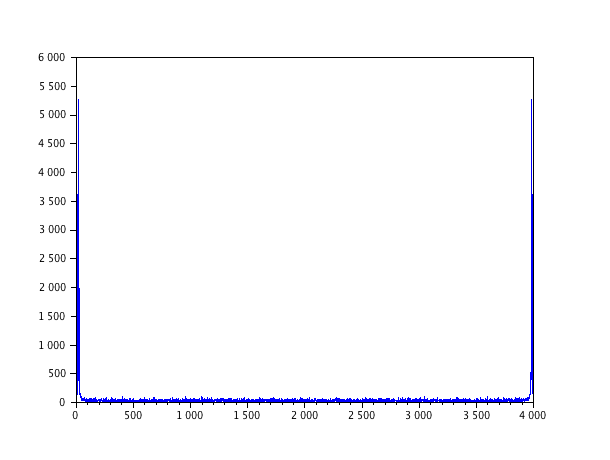
Le spectre est symétrique par rapport à l'axe vertical qui passe par l'abscisse i=N/2
Remarque :
Nous avons dit qu'on n'est rarement amené à calculer une intégrale de Fourier directement. Quelquefois, le calcul direct est délicat voire très difficile. Il est quelquefois plus astucieux d'exploiter les propriétés pour déterminer indirectement une transformée de Fourier. Nous avons vu par calcul direct la transformée de Fourier de la fonction porte (la seule d'ailleurs que nous avons calculé directement) :
or, la fonction porte et la fonction sinus cardinal sont toutes les deux paires (la transformée de Fourier conserve la parité). Moyennant cette remarque, il devient aisé de déterminer la transformée de Fourier suivante :
en exploitant la relation démontrée plus haut, soit : 
En effet, si on prend 
alors 
Nous venons de rappeler que
donc finalement 
Remarque :
Il faut ici jongler avec les espaces duaux comme on l'a déjà fait remarquer : la transformée de Fourier réciproque pour un signal temporel a peu de sens pour le physicien (
) ; pour le mathématicien, cette transformée inverse conduit à une fonction de la fréquence.
Relations de Parseval
Nous les donnons sans démonstration rigoureuse. Par contre, nous les interprétons aisément dans le cadre de l'interprétation géométrique de la transformée de Fourier en tant que changement de base dans l'espace de travail (
ou plutôt 
ou bien 
). L'idée des relations de Parseval est que le changement de base conserve le produit scalaire. Qu'il soit exprimé dans l'espace direct ou dans l'espace réciproque, le produit scalaire de deux signaux – vecteurs est le même, soit :
et ce, que le temps soit discret ou continu. Pour des signaux de
, ça donne :
Le cas particulier 
est important puisqu'il conduit à exprimer l'énergie du signal respectivement décrit dans l'espace direct ou dans l'espace réciproque :
soit,
