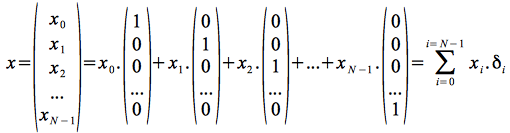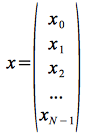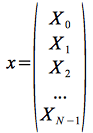Transformation de Fourier discrète
La transformée de Fourier d'un signal ou d'un vecteur de 
n'est rien d'autre que l'expression de ce même vecteur dans une autre base de l'espace 
que celle dite canonique qui fonde l'équation :
Le nouvel ensemble des vecteurs qui forment cette nouvelle base est défini par les vecteurs de dimension N qui sont obtenus par échantillonnage des N fonctions exponentielles complexes 
, où T est la durée du vecteur, soit 
avec 
, période d'échantillonnage et 
.
Les N exponentielles à échantillonner peuvent se réécrire moyennant les résultats précédents :
puisque les valeurs échantillonnées du temps t continu deviennent 
On admet d’ailleurs qu'il s'agit bien d'une base orthogonale de .
Il s'agit de bien comprendre qu'on exprime le vecteur d'origine dans le même espace sans perte de dimension c'est-à-dire, sans perte d'information. Il est initialement exprimé dans la base canonique selon les coordonnées,
soit avec N coordonnées ou composantes en tant que vecteur de 
.
Après transformation de Fourier, il sera représenté selon toujours N composantes ou coordonnées mais cette-fois ci complexes, comme combinaison linéaire des vecteurs exponentielles complexes, selon,
Il convient à présent d'établir les équations qui permettent de passer des coordonnées dans la base canonique ou espace de départ, à la base des exponentielles complexes ou espace d'arrivée (bien qu'en toute rigueur espace de départ et espace d'arrivée sont identiques).
Si on se reporte aux équations de changement de base rappelées dans le paragraphe précédent, il convient de projeter le vecteur d'origine, 
dans les rappels, maintenant 
sur les vecteurs qui définissent le nouvel ensemble des vecteurs de base. La dimension du problème étant N, il y a N projections à opérer. Les équations correspondantes définissent la transformation de Fourier discrète du vecteur :
Remarque :
Dans la mesure où le second opérande du produit scalaire est complexe, il faut le conjuguer (cf. chapitre précédent). D'où l'apparition du signe négatif dans l'exponentielle dans le membre de droite.
Remarque :
Les composantes sont complexes, l'espace de départ est donc en réalité 
et non 
. Par contre, un signal physique échantillonné sauf extraordinaire conduit bien à un vecteur de 
. Toutefois si on en calcule la transformée de Fourier discrète, on obtient généralement un vecteur de 
. Souvent, on représente graphiquement la transformée de Fourier d'un signal par son module mais il ne faut jamais oublier qu'il y a généralement une partie imaginaire. Voilà qui doit vous rappeler le diagramme de Bode qui est aussi une fonction complexe de la fréquence. De fait, il y a un lien étroit entre transformation de Fourier et fonction de transfert d'un filtre, nous y reviendrons dans le chapitre suivant.
Si on écrit à présent le signal d'origine comme combinaison linéaire des exponentielles complexes avec les poids 
, on obtient, composante par composante :
formule que nous admettrons et qui définit la transformation de Fourier discrète inverse. Elle permet à partir des composantes issues de la transformée de Fourier directe de reconstituer le vecteur d'origine dans la base canonique. La transformée de Fourier directe et inverse forment donc un couple de transformations réciproques, réversibles qui traduit le fait qu'il n'y a pas de perte d'information : il s'agit bien du même vecteur mais exprimé dans deux bases différentes toutefois de même dimensions.
Remarque :
En réalité, les exponentielles complexes échantillonnées qui définissent le nouvel ensemble de vecteurs de base sont bien orthogonales deux à deux mais pas normées, d'où le coefficient
dans la définition de la transformée inverse. En fait, on a arbitrairement affecté ce coefficient à la transformée inverse mais on pourrait pu tout aussi bien l'affecter à la transformée directe voire affecter le même coefficient
à la fois à la transformée directe et inverse. Il importe que les deux transformée soient bien réciproques l'une de l'autre mais la position précise du ou des coefficients est arbitraire.
La vidéo ci-dessous montre la pertinence de représenter un signal dans l'espace fréquentiel où il devient beaucoup plus intelligible. Le traitement de débruitage qui est exposé permet aussi une opération capitale en signal : la compression.
Le Lien ci-dessous permet de télécharger le fichier son pour appliquer les traitements décrits dans les vidéos ci-dessus.
