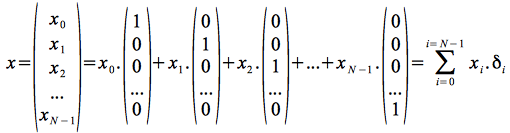Premier contact
Pour donner une signification en l’occurrence géométrique à la transformation de Fourier, on part de la représentation vectorielle du chapitre précédent d'un signal de ![]() et on rappelle les équations fondamentales que nous y avons découverts.
et on rappelle les équations fondamentales que nous y avons découverts.
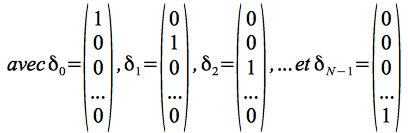
Sous cette forme, le signal échantillonné peut être interprété comme étant un vecteur dans un espace vectoriel de dimension N. L'équation précédente est donc lue comme la représentation du vecteur du signal dans la base canonique des vecteurs![]() qui forme un ensemble de vecteurs orthonormés, une base de l'espace des signaux de
qui forme un ensemble de vecteurs orthonormés, une base de l'espace des signaux de ![]() .
.
Pour bien s'approprier le concept nouveau, il n'est pas inutile de se remettre en tête une notion classique dont la transformation de Fourier est une extension. Nous allons donc reprendre un peu les questions de représentation vectorielle dans ![]() et la question ici centrale de changement de repère puis nous généraliserons assez aisément à
et la question ici centrale de changement de repère puis nous généraliserons assez aisément à ![]() . Si on considère l'espace vectoriel
. Si on considère l'espace vectoriel ![]() muni d'une base orthonormée
muni d'une base orthonormée ![]() , alors un vecteur
, alors un vecteur ![]() quelconque de cet espace vectoriel s'écrira :
quelconque de cet espace vectoriel s'écrira :
![]() qu'on écrit aussi :
qu'on écrit aussi : 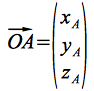 .
.
Il est clair que les vecteurs![]() ont dans la base qu'ils forment respectivement les coordonnées :
ont dans la base qu'ils forment respectivement les coordonnées :![]() ,
, ![]() et
et ![]() .
.
Nous savons toutefois que la base ![]() n'est pas la seule possible. En fait, il existe une infinité de bases orthonormées de triplets de vecteurs unitaires deux à deux orthogonaux et on passe de l'une à l'autre moyennant trois rotations. Si on définit une nouvelle base par les trois vecteurs orthonormés
n'est pas la seule possible. En fait, il existe une infinité de bases orthonormées de triplets de vecteurs unitaires deux à deux orthogonaux et on passe de l'une à l'autre moyennant trois rotations. Si on définit une nouvelle base par les trois vecteurs orthonormés ![]() ,alors le vecteur
,alors le vecteur ![]() s'écrira dans cette base,
s'écrira dans cette base, ![]()
Il faut insister sur le fait que les coordonnées dans cette nouvelle base ont changé mais c'est le même vecteur qui est pourvu dans cette nouvelle base d'une nouvelle représentation. Pour obtenir ces nouvelles coordonnées, on procède comme suit : on exprime toutes les coordonnées dans la base initiale ![]() , soit les coordonnées de
, soit les coordonnées de ![]() et les coordonnées dans
et les coordonnées dans ![]() des vecteurs
des vecteurs ![]() qui définissent la nouvelle base.
qui définissent la nouvelle base.
Alors, ![]()
puisque le triplet ![]() est orthonormé.
est orthonormé.
De façon analogue, on obtient :
![]()
![]()
![]()
On interprète ces équations de la manière suivante : on obtient les coordonnées du vecteur dans la nouvelle base en projetant ce vecteur sur les vecteurs de cette nouvelle base.