Lois de Snell Descartes

Les lois de Snell-Descartes concernent le comportement d'un rayon lumineux arrivant sur une surface réfléchissante ou traversant un dioptre (de forme quelconque) séparant deux milieux transparents différents.

Dans le premier cas, il y a formation d'un rayon réfléchi.

Dans le second cas, le rayon incident est en général divisé en un rayon réfléchi et un rayon réfracté.

1re loi : loi du plan d'incidence :

Le rayon réfléchi et le rayon réfracté sont dans le plan d'incidence. Le plan d'incidence est le plan qui contient le rayon incident et la normale à la surface de séparation.

2e loi : loi de la réflexion :

Les rayons incidents et réfléchis forment des angles égaux avec la normale à la surface de séparation.

3e loi : loi de la réfraction :

Les rayons incidents et réfractés se trouvent de part et d'autre de la normale au dioptre et forment avec celle-ci les angles respectifs i1 et i2 tels que :

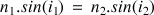(17)

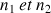sont les indices de réfraction des deux milieux 1 et 2 séparés par le dioptre.

Remarque : si le rayon incident n'est pas monochromatique, l'angle 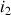dépend de la longueur d'onde car les indices 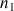et 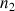en dépendent. Cette dépendance étant faible, on pourra quand même employer une source de lumière blanche.

Dans l'étude de la réfraction, deux cas sont à envisager :

1. le second milieu est dit plus réfringent que le premier :

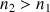
   Comment est l'angle de réfraction par rapport à l'angle d'incidence ? Quelle est la valeur limite

   maximale prise par i2 en fonction des indices de réfraction des deux milieux ?

2. le second milieu est moins réfringent que le premier :

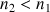
   Comment est l'angle de réfraction par rapport à l'angle d'incidence ?

   Quelle est la valeur maximale de 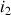? La valeur de 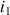associée est appelée angle limite d'incidence

   et est parfois notée .

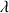   Que se passe-t-il lorsque 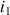est supérieur à 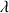? En déduire une méthode pour déterminer l'indice 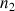connaissant .
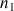