Travail demandé
Il s'agit d'étudier le comportement thermodynamique d'un gaz emprisonné dans un tube cylindrique de section S = 1.02 10-4 m2. La pression P de ce gaz est la somme de la pression atmosphérique (Patm) et de la pression due à la dénivellation du mercure (
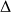 P) :
P) :
P = Patm + P = Patm +
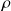 gh
gh
avec :
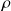 : masse volumique du mercure = 13600 Kg/m3.
: masse volumique du mercure = 13600 Kg/m3.
g : accélération de la pesanteur = 9.81 m/s2.
h : hauteur de la colonne du mercure (m).
1. Travail théorique
Pour le gaz utilisé dans l'expérience, le coefficient de dilatation isobare varie avec la température suivant la loi :
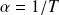 .
.
Donner après intégration, la forme de l'équation d'état du gaz.
2. Travail pratique
Partie A
a) Déterminer, à partir du baromètre de mercure installé dans la salle de travaux pratiques, la valeur de la pression atmosphérique Patm.
A température constante, faites varier progressivement la pression du gaz (en variant h) et relever le volume correspondant (en lisant la longueur l de la colonne d'air). Remplir le tableau I ci-dessous pour huit valeurs différentes de P :
Patm = (Pa) | ||||||||
| ||||||||
h (m) | ||||||||
P = Patm +
| ||||||||
l (m) | ||||||||
V = S . l (m3) | ||||||||
PV (Joule) |
b) Tracer la courbe P = f(V). Peut-on trouver facilement une relation simple entre ces deux grandeurs ? Justifier votre réponse.
c) Tracer la courbe de variation de P en fonction de 1/V. Peut-on trouver cette fois ci, une relation simple entre ces deux grandeurs? Justifier votre réponse.
d) En supposant que le gaz est parfait, déterminer une valeur approchée de la constante R des gaz parfaits (se servir de la pente de la courbe P = f(1/V) et du nombre de moles n du gaz).
e) Déterminer l'erreur relative par rapport à la valeur théorique : |R - Rth| / Rth. Conclure.
Partie B
a) Remplir le tableau II ci-dessous en donnant pour chaque couple (P, V), le coefficient de compressibilité isotherme correspondant qui sera calculé graphiquement selon la manière indiquée sur la figure suivante :
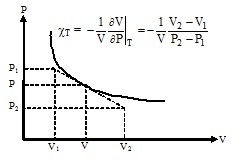
Figure 2 : Méthode de détermination graphique de
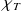
P (Pa) | ... | ... | ||||||
1/P (Pa-1) | ... | ... | ||||||
| ... | ... |
b) Tracer la courbe
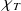 = f(1/P). En déduire la pente de la courbe et l'expression analytique de
= f(1/P). En déduire la pente de la courbe et l'expression analytique de
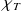 .
.
c) En se basant sur ce résultat et sur la partie théorique, déterminer l'expression de l'équation d'état du gaz considéré. On donne :
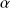 = 1/T
= 1/T