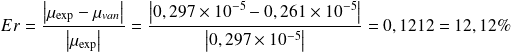Présentation des résultats
Pour les deux types de gaz (CO2 et N2), on représente dans les tableaux ci-dessous les valeurs mesurées des paires (ΔP-ΔT).
ΔP(KPa) | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 | 0 |
ΔT(K) | 0.52 | 0.5 | 0.4 | 0.43 | 0.39 | 0.3 | 0.17 | 0.08 | -0.01 | -0.06 |
ΔP(KPa) | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 | 0 |
ΔT(K) | 0.11 | 0.07 | 0.01 | -0.01 | -0.03 | -0.06 | -0.1 | -0.13 | -0.14 | -0.16 |
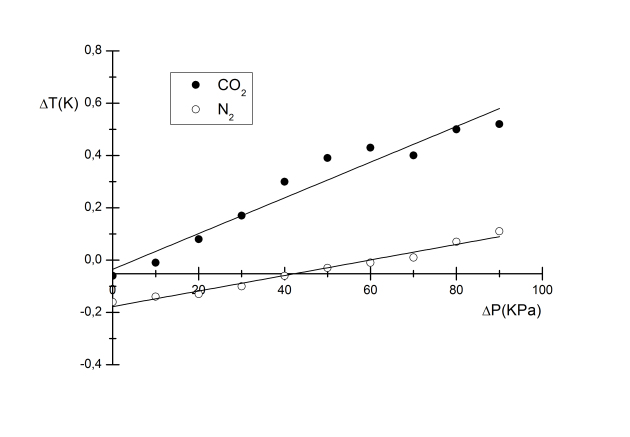
La variation de ΔT en fonction de ΔP [ΔT = f (ΔP)] est représentée sur la figure suivante pour les deux gaz : CO2 et N2. Les valeurs expérimentales sont représentées par des points solides ou cercles alors que les courbes de tendances (courbes approchées) y sont associées sont représentées par des lignes solides.
Valeurs expérimentales du coefficient de Joule-Thomson, µ.
La pente de la courbe, ΔT = f (ΔP), représente le coefficient, µ, obtenu expérimentalement µ :
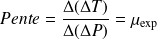
- Pour CO2 :
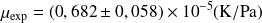
- Pour CO2 :
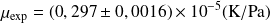
Valeurs du coefficient de Joule-Thomson, µ, en adoptant le modèle de Van Der Waales.
- Pour un gaz assimilé à un gaz réel du Van Der Waals, le coefficient, µ, est exprimé par :
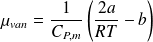
- Cp,m : la capacité calorifique molaire à pression constante du gaz (à P et T bien déterminées) ; a et b : les coefficients de Van Der Waals du gaz considéré.
- L'expérience se fait à P = 1000,5 hPa = 100050 Pa ≈ 1bar et T = 293.7 K.
- Pour le cas de CO2
a = 3,6 (Pa.m6/mol2) ; b = 42,7 (cm3/mol) ; CPm = 366,1 (J/mol.K)
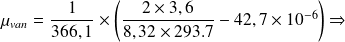
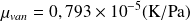
- Pour le cas de N2
a = 0,1408 Pa.m6/mol2 ; b = 39,13 cm3/mol ; CPm = 29,1 J/mol.K
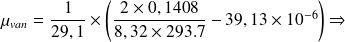
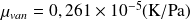
Validité du modèle de Van Der Waals pour le calcul du coefficient de Joule-Thomson.
Pour ce fait, on calcule l'erreur relative commise lors du calcul du coefficient de Joule-Thomson en assimilant le gaz à celui de Van Der Waals.
Pour CO2 :
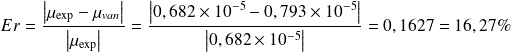
Pour N2 :