Exemples de paramétrages

On considère l'exemple : .

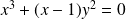Etude de fonction
On peut remarquer que 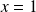ne conduit à aucune solution, donc que l'équation équivaut à : .
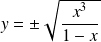Donc on peut étudier la fonction 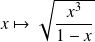et symétriser la courbe par rapport à l'axe des abscisses.
Paramétrage cartésien
On peut remarquer que si 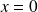, alors 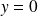. Et si 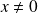, on pose : .
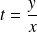En divisant par 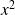, l'équation devient : 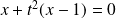, donc .
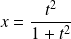Donc la courbe 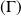est la courbe d'équation 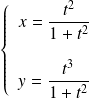puisque le cas 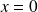est obtenu pour .
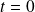Paramétrage polaire
On pose 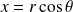et .
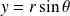L'équation s'écrit : 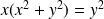, donc : .
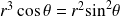On peut remarquer que si 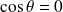, alors 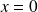et .
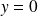Donc la courbe 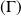est la courbe d'équation 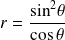puisque le point 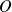est obtenu pour .
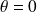