Montrons par récurrence que :
.
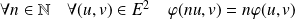Initialisation :
.
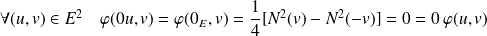Donc la propriété est vraie pour
.
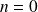Hérédité : Soit
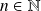tel que
.
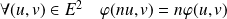Donc :
.
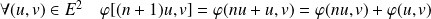Donc :
.
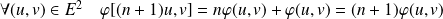Conclusion :
.
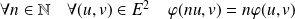De plus :
.
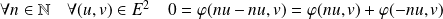Donc :
.
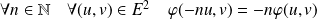Donc :
.
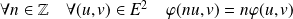Soit
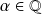. Donc il existe
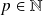et
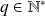tels que :
.
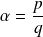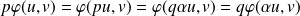. Donc :
.
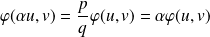Donc :
.
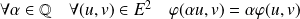Soit
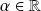. Il existe une suite de rationnels
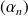qui converge vers
.
.
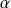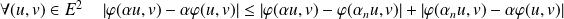Donc :
.
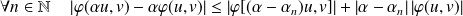Le deuxième terme tend vers
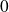quand
tend vers l'infini.
Etudions le premier terme :
.
.
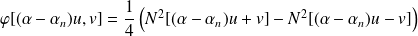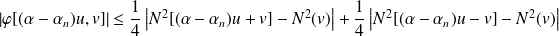Or, d'après les propriétés des normes :
.
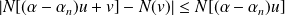Donc :
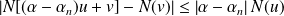. Donc
.
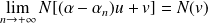De même :
.
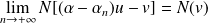Donc le premier terme tend aussi vers
:
.
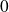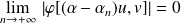Donc
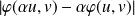est un terme positif majoré par une suite qui converge vers
.
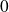Conclusion :
.
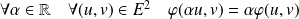